题目内容
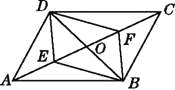
【题目】如图,在ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当点E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )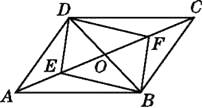
A.OE=OF
B.DF=BE
C.AE=CF
D.∠AEB=∠CFD
【答案】B
【解析】解:A、∵ABCD
∴OB=OD
∵OE=OF
∴四边形DEBF是平行四边形,因此A不符合题意;
B、添上条件DF=BE,不能证明四边形DEBF是平行四边形;因此B符合题意;
C、∵ABCD
∴OB=OD,OA=OC
∵AE=CF
∴OE=OF ∵OB=OD
∴四边形DEBF是平行四边形,因此C不符合题意;
D、∵ABCD
∴AB=CD,AB∥CD
∴∠EAB=∠FCD
在△AEB和△CFD中
∴△AEB≌△CFD
∴BE=DF,
∵∠AEB=∠CFD
∴∠AEB+∠BEO=180°,∠CFD+∠DFO=180°
∴∠BEO=∠DFO
∴BE∥DF,∵BE=DF,
∴四边形DEBF是平行四边形,因此D不符合题意;
故答案为:B
根据平行四边形的判定及全等三角形的判定和性质,结合题中的选项,逐一进行判断即可。

练习册系列答案
相关题目