��Ŀ����
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm����BAC=60��������M�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����N�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
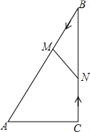
��1����BM=BN����t��ֵ��
��2������MBN���ABC���ƣ���t��ֵ��
��3����tΪ��ֵʱ���ı���ACNM�������С���������Сֵ��
���𰸡���1��10![]() -15����2��t=
-15����2��t=![]() ��t=
��t=![]() ����3��t=2.5����СֵΪ
����3��t=2.5����СֵΪ![]()
�������������������1������Rt��ABC�����ʵó�AB��BC�ij��ȣ�Ȼ�����BM=BN�ó�t��ֵ����2������MBN�ס�ABC����NBM�ס�ABC��������ֱ����t��ֵ����3�������ı��ε����������ABC�������ȥ��BMN������ó���������ʽ���Ӷ������ֵ.
�����������1������Rt��ABC����ACB=90����AC=5����BAC=60������![]() ��
��![]()
������֪![]() ��
��![]() ��
��![]() �� ��BM=BN��
�� ��BM=BN��![]()
��ã�![]()
��2��������MBN�ס�ABCʱ�� ��![]() ����
����![]() ����ã�
����ã�![]()
������NBM�ס�ABCʱ�� ��![]() �� ��
�� ��![]() ����ã�
����ã�![]() ��
��
����![]() ��
��![]() ʱ����MBN����ABC���ƣ�
ʱ����MBN����ABC���ƣ�
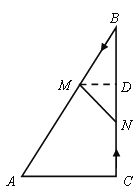
��3����M��MD��BC�ڵ�D���ɵã�![]() ���ı���ACNM�����Ϊ
���ı���ACNM�����Ϊ![]() ��
��
��![]()
![]()
![]()
![]() ��
��
�����ݶ��κ��������ʿ�֪����![]() ʱ��
ʱ��![]() ��ֵ��С�� ��ʱ��
��ֵ��С�� ��ʱ��![]()

����Ŀ��ijˮ�����������㽶����(ǧ��)���ۼ�(Ԫ)֮��Ĺ�ϵ���±���
�㽶����(ǧ��) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | �� |
�ۼ�(Ԫ) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | �� |
�ϱ���ӳ����������֮��Ĺ�ϵ�����У��Ա�����________���������________��