题目内容
【题目】如图,ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.
求证:四边形AECF是平行四边形.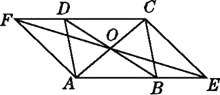
【答案】证明:∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC.
∵AB∥CD,
∴∠DFO=∠BEO,∠FDO=∠EBO.
在△FDO和△EBO中,
∠DFO=∠BEO,∠FDO=∠EBO,OD=OB,
∴△FDO≌△EBO(AAS).
∴OF=OE.
∴四边形AECF是平行四边形
【解析】根据平行四边形的性质得出OD=OB,OA=OC,再根据AB∥CD得出∠DFO=∠BEO,∠FDO=∠EBO,就可证明△FDO≌△EBO,从而证得OF=OE,然后根据对角线互相平分的四边形是平行四边形,即可证得结论。

练习册系列答案
相关题目