题目内容
【题目】如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变.
那么,你认为( )

A. 甲、乙都对 B. 乙对甲不对 C. 甲对乙不对 D. 甲、乙都不对
【答案】A
【解析】
连接DF、AF、CD(如图),证明△BDF为等边三角形,即可得∠DBF=60°,再证明△ABF绕点B顺时针旋转60°可得到△CBD,即可得AF=CD,∠FAB=∠DCB,甲的说法正确;因为∠FAB+∠AMN+∠ANM=∠DCB+∠ABC+∠BNC=180°,∠ANM=∠BNC,即可得∠AMN=∠ABC=60°,乙的说法正确.
连接DF、AF、CD,如图,
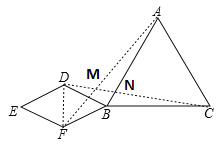
四边形BDEF为菱形,
∴BD=BF,
∵DF=BD,
∴BD=BF=DF,
∴△BDF为等边三角形,
∴∠DBF=60°,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴∠ABF=∠CBD,
∴△ABF绕点B顺时针旋转60°可得到△CBD,
∴AF=CD,∠FAB=∠DCB,
∴∠FAB+∠AMN+∠ANM=∠DCB+∠ABC+∠BNC=180°,
∵∠ANM=∠BNC,
∴∠AMN=∠ABC=60°,
即直线AF和直线CD所夹的锐角的度数为60°.
综上,甲、乙的结论都对.
故选A.

【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
(1)(收集数据)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是________.
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
(2)(整理数据)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
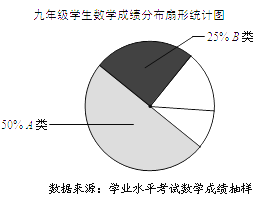
①C类和D类部分的圆心角度数分别为________°、________°;
②估计九年级A、B类学生一共有________名.
(3)(分析数据)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.





