题目内容
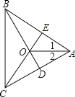
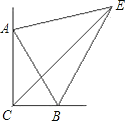
【题目】如图,△ABC中,AB=AC, ,∠C==30°,DA⊥BA于点A,BC=16cm, 则AD=__.

【答案】![]()
【解析】
根据等边对等角可得∠B=∠C,再利用三角形的内角和定理求出∠BAC=120°,然后求出∠CAD=30°,从而得到∠CAD=∠C,根据等角对等边可得AD=CD,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AD,然后根据BC=BD+CD列出方程求解即可.
解:∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°-2×30°=120°,
∵DA⊥BA,
∴∠BAD=90°,
∴∠CAD=120°-90°=30°,
∴∠CAD=∠C,
∴AD=CD,
在Rt△ABD中,∵∠B=30°,∠BAD=90°,
∴BD=2AD,
∴BC=BD+CD=2AD+AD=3AD,
∵BC=16cm,
∴AD=![]() cm.
cm.

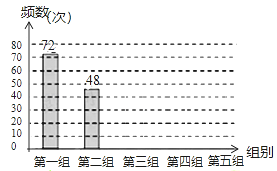
【题目】某网络约车公司近期推出了”520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图(如图).
组别 | 单次营运里程“x“(公里) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据统计表、图提供的信息,解答下面的问题:
(1)①表中a= ;②样本中“单次营运里程”不超过15公里的频率为 ;③请把频数分布直方图补充完整;
(2)请估计该公司这5000个“单次营运里程”超过20公里的次数;
(3)为缓解城市交通压力,维护交通秩序,来自某市区的4名网约车司机(3男1女)成立了“交通秩序维护”志愿小分队,若从该小分队中任意抽取两名司机在某一路口维护交通秩序,请用列举法(画树状图或列表)求出恰好抽到“一男一女”的概率.