Question

【题目】阅读材料1：

对于两个正实数，由于，所以，即，所以得到，并且当时，

阅读材料2：

若，则 ，因为，，所以由阅读材料1可得：，即的最小值是2，只有时，即=1时取得最小值.

根据以上阅读材料，请回答以下问题：

(1)比较大小

(其中≥1)； -2(其中<-1)

(2)已知代数式变形为，求常数的值

(3)当= 时，有最小值，最小值为 (直接写出答案).

Answer 1

【答案】（1）；（2）；（3）0，3．

【解析】

（1）根据求差法比较大小，由材料1可知将结果用配方法变形即可得出结论.

（2）根据材料（2）的方法，把代数式变形为，解答即可；

（3）先将变形为,由材料（2）可知时（即x=0，）有最小值．

解：（1），所以；

当时，由阅读材料1可得，，

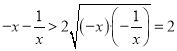所以；

（2）

，

所以；

（3）

∵x≥0，

∴

即：当时，有最小值，

∴当x=0时，有最小值为3.