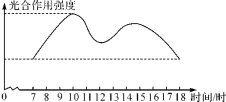
题目内容
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.

【答案】(1)画图见解析;(2)∠PP′C=30°.
【解析】
(1)如图,作∠PAP′=50°,且AP=AP′,连接PP′,△ACP′即为所求;(2),连接PP′,由旋转的性质可得,∠PAP′=∠BAC=50°,AP=AP′,△ABP≌△ACP′,根据等腰三角形的性质及三角形的内角和定理可得∠APP′=∠AP′P=65°,根据全等三角形的性质可得∠AP′C=∠APB,在△ABC中,∠BAC=50°,AB=AC,可求得∠B=65°,再由∠BAP=20°,根据三角形的内角和定理求得∠APB=95°=∠AP′C,所以∠PP′C=∠AP′C-∠AP′P=30°.
(1)旋转后的△ACP′如图所示.
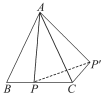
(2)如图,连接PP′.
由旋转可得,∠PAP′=∠BAC=50°,AP=AP′,△ABP≌△ACP′,
∴∠APP′=∠AP′P=65°,∠AP′C=∠APB,
∵∠BAC=50°,AB=AC,
∴∠B=65°,
又∵∠BAP=20°,
∴∠APB=95°=∠AP′C,
∴∠PP′C=∠AP′C-∠AP′P=95°-65°=30°.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目