题目内容
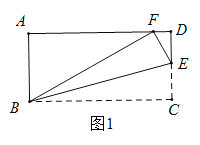
【题目】如图1.已知四边形![]() 是矩形.点
是矩形.点![]() 在
在![]() 的延长线上.
的延长线上.![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]()
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,求
,求![]() 的长;
的长;
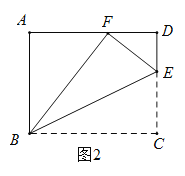
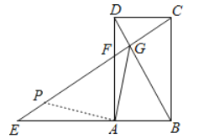
![]() 如图2,连接
如图2,连接![]() ,求证:
,求证:![]() .
.
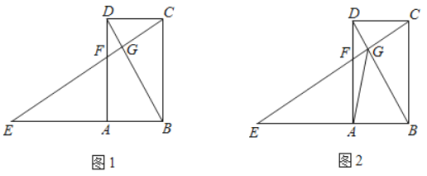
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由矩形的形及已知证得△EAF≌△DAB,则有∠E=∠ADB,进而证得∠EGB=90即可证得结论;
(2)设AE=x,利用矩形性质知AF∥BC,则有![]() ,进而得到x的方程,解之即可;
,进而得到x的方程,解之即可;
(3)在EF上截取EH=DG,进而证明△EHA≌△DGA,得到∠EAH=∠DAG,AH=AG,则证得△HAG为等腰直角三角形,即可得证结论.
(1)∵四边形ABCD是矩形,
∴∠BAD=∠EAD=90,AO=BC,AD∥BC,
在△EAF和△DAB,
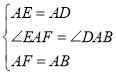 ,
,
∴△EAF≌△DAB(SAS),
∴∠E=∠BDA,
∵∠BDA+∠ABD=90,
∴∠E+∠ABD=90,
∴∠EGB=90,
∴BG⊥EC;
(2)设AE=x,则EB=1+x,BC=AD=AE=x,
∵AF∥BC,∠E=∠E,
∴△EAF∽△EBC,
∴![]() ,又AF=AB=1,
,又AF=AB=1,
∴![]() 即
即![]() ,
,
解得:![]() ,
,![]() (舍去)
(舍去)
即AE=![]() ;
;
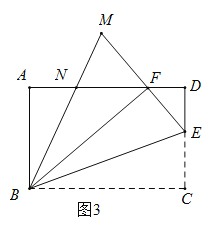
(3)在EG上截取EH=DG,连接AH,
在△EAH和△DAG,
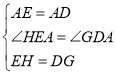 ,
,
∴△EAH≌△DAG(SAS),
∴∠EAH=∠DAG,AH=AG,
∵∠EAH+∠DAH=90,
∴∠DAG+∠DAH=90,
∴∠EAG=90,
∴△GAH是等腰直角三角形,
∴![]() 即
即![]() ,
,
∴GH=![]() AG,
AG,
∵GH=EG-EH=EG-DG,
∴![]() .
.

【题目】某公园的门票价格如表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b(a≥b).若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则共需支付门票费为990元,那么这两个部门的人数a=_____;b=_____.