题目内容
【题目】如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则△PMN周长的最小值是_______.

【答案】9
【解析】
要求PM+PN的最小值,PM、PN不能直接求,可考虑通过作辅助线转化PN、PM的值,从而找出其最小值,即可求出△PMN周长的最小值.
解:如图:连接MN,作ME⊥AC交AD于E,连接EN,
则EN就是PM+PN的最小值,
∵菱形ABCD,M、N分别是AB、BC的中点,
∴BN=BM=AM,MN=![]()
∵ME⊥AC交AD于E,
∴AE=AM,
∴AE=BN,AE∥BN,
∴四边形ABNE是平行四边形,
∴EN=AB,EN∥AB,
而由题意可知,可得AB=![]() =5,
=5,
∴EN=AB=5,
∴PM+PN的最小值为5.
∵MN不变,当PM+PN的最小值时,△PMN周长最小 ,
∴△PMN周长最小=9
故答案为:9.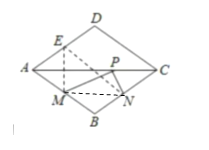

练习册系列答案
相关题目