题目内容
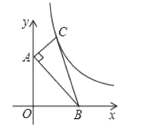
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,点
,点![]() 在第一象限内,
在第一象限内,![]() ,
,![]() ,函数
,函数![]() 的图像经过点
的图像经过点![]() ,将
,将![]() 沿
沿![]() 轴的正方向向右平移
轴的正方向向右平移![]() 个单位长度,使点
个单位长度,使点![]() 恰好落在函数
恰好落在函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
【答案】C
【解析】
作CH⊥y轴于H.由相似三角形的性质求出点C坐标,进而求出k的值,依据反比例函数图象上点的坐标特征即可解决问题;
解:如图,作CH⊥y轴于H.
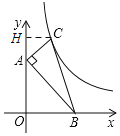
∵A(0,4)、B(4,0),
∴OA=OB=4,
∵∠BAC=90°,
∴∠OAB+∠CAH=90°,
∵∠ABO+∠OAB=90°,
∴∠ABO=∠CAH,
又∵∠AOB=∠AHC=90°,
∴△ABO∽△CAH,
∴![]() ,
,
∴![]()
∴CH=AH=2,
∴OH=OA+AH=6,
∴C(2,6),
∵点C在![]() 的图象上,
的图象上,
∴k=2×6=12,
∴![]() ,
,
∴当y=4时,x=3,
∵将△ABC沿x轴的正方向向右平移m个单位长度,使点A恰好落在函数![]() 的图象上,
的图象上,
∴m=3,
故选:C.

练习册系列答案
相关题目