[题目]如图.△ABC中.AB=BC.BE⊥AC于点E.AD⊥BC于点D.∠BAD=45°.AD与BE交于点F.连接CF.(1)求证:BF=2AE,(2)若CD=1.求AD的长. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF.

(1)求证：BF=2AE；(2)若CD=1，求AD的长.

【答案】（1）证明见解析（2）

【解析】

(1)先利用等腰直角三角形的性质及角的等量替换证明△ADC≌△BDF，得到BF=AC再根据等腰三角形三线合一得出AC=2AE，即可得证；

（2）在在Rt△CDF，利用勾股定理求出CF，再利用等腰三角形的性质得AF=CF，即可求出AD.

(1)证明：∵AD⊥BC，∠BAD=45°，

∴△ABD是等腰直角三角形，

∴AD=BD，

∵BE⊥AC，AD⊥BC，

∴∠CAD+∠ACD=90°，∠CBE+∠ACD=90°，

∴∠CAD=∠CBE，

在△ADC和△BDF中，，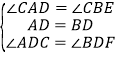

∴△ADC≌△BDF(ASA)，

∴BF=AC，

∵AB=BC，BE⊥AC，

∴AC=2AE，

∴BF=2AE；

(2)解：∵△ADC≌△BDF，

∴DF=CD=1，

在Rt△CDF中，CF=

∵BE⊥AC，AE=EC，

∴AF=CF=，

∴AD=AF+DF=1+.

练习册系列答案

【题目】如图，在△ABC中，AD为∠BAC的平分线，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC交AC的延长线于F．

（1）求证：BE=CF；
（2）如果AB=7，AC=5，求AE，BE的长．

【题目】如图，△ABC为等边三角形，点E在BA的延长线上，点D在BC边上，且ED＝EC，若△ABC的边长为4，AE＝2，则BD的长为( )

A. 2 B. 3 C. D. ＋1

【题目】如图，已知，线段m，用尺规作图作菱形ABCD，使它的边长为m，一个内角等于其具体步骤如下：

作；

以点A为圆心，线段m长为半径画弧，交AE于点B，交AF于点D；

__________；

连接BC、DC，则四边形ABCD为所作的菱形第步应为　　

A. 分别以点B、D为圆心，以AF长为半径画弧，两弧交于点C

B. 分别以点E、F为圆心，以AD长为半径画弧，两弧交于点C

C. 分别以点B、D为圆心，以AD长为半径画弧，两弧交于点C

D. 分别以点E、F为圆心，以AF长为半径画弧，两弧交于点C

【题目】如图，在△ABC中，∠CBD、∠BCE是△ABC的外角，BP平分∠ABC，CP平分∠ACB，BQ平分∠CBD，CQ平分∠BCE．

（1）∠PBQ的度数是　　，∠PCQ的度数是　　；

（2）若∠A＝70°，求∠P和∠Q的度数；

（3）若∠A＝α，则∠P＝　　，∠Q＝　　（用含α的代数式表示）．

【题目】（问题）
如图1，在Rt△ABC中，∠ACB=90°，AC=BC，过点C作直线l平行于AB．∠EDF=90°，点D在直线l上移动，角的一边DE始终经过点B，另一边DF与AC交于点P，研究DP和DB的数量关系．

（探究发现）
（1）如图2，某数学兴趣小组运用“从特殊到一般”的数学思想，发现当点D移动到使点P与点C重合时，通过推理就可以得到DP=DB，请写出证明过程；
（数学思考）
（2）如图3，若点P是AC上的任意一点（不含端点A、C），受（1）的启发，这个小组过点D作DG⊥CD交BC于点G，就可以证明DP=DB，请完成证明过程；
（拓展引申）
（3）如图4，在（1）的条件下，M是AB边上任意一点（不含端点A、B），N是射线BD上一点，且AM=BN，连接MN与BC交于点Q，这个数学兴趣小组经过多次取M点反复进行实验，发现点M在某一位置时BQ的值最大．若AC=BC=4，请你直接写出BQ的最大值．