Question

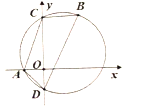
【题目】如图，在平面直角坐标系中，，，经过两点的圆交轴于点（在上方），则四边形面积的最小值为__________．

Answer 1

【答案】

【解析】

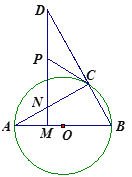
四边形ADBC的面积分两部分，是△ADC和△BDC的面积和，两个三角形计算面积时，都以CD为底，点A到CD 的 距离为2，点B到CD 的 距离为3，这两个高是定值，所以只有当底CD值最小时，四边形ADBC的面积才有最小值.根据垂径定理知，弦的垂直平分线必过圆心，所以求出过圆心和线段AB中点的直线l的解析式，再根据勾股定理得出关于CH的关系式，先求得CD的一半，即CH的最小值，从而求出CD 的最小值.

解：如图：

∵，，

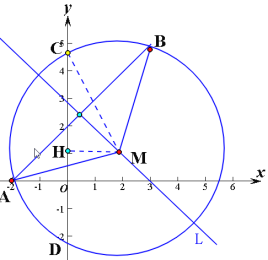
∴AB的中点坐标为（ ，），AB与x轴夹角为45°，设圆心为M，

线段AB的垂直平分线l必过圆心M，解得l的解析式为y=-x+3，设圆心M的横坐标为a，则纵坐标为：-a+3，即M（a，-a+3）,半径r2=(a+2)2+(a-3)2

∴S四边形ADBC=×OA×CD +×yB×CD=×2×CD +×3×CD=CD,

当CD值最小时，S四边形ADBC有最小值.

∵Rt△CMH中，由勾股定理得：CH2=CM2-MH2=(a+2)2+(a-3)2-a2=a2-2a+13=(a-1)2+12，

当a=1时，CH2有最小值，为12，即CH=2，CD=2CH=4，

∴S四边形ADBC最小值=×4=10 .

故答案为：10 .