题目内容

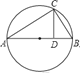
【题目】已知内接于⊙O.

(1)当点O与AB有怎样的位置关系时，∠ACB是直角.

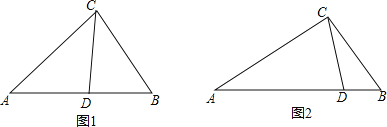
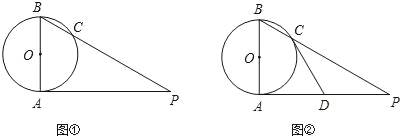
(2)在满足(1)的条件下，过点C作直线交AB于D，当CD与AB有什么样的关系时，△ABC∽△CBD∽△ACD.请画出符合(1)、(2)题意的两个图形后再作答.

【答案】(1)点O在AB上时，∠ACB是直角；(2)CD与AB垂直相交于D时，△ABC∽△CBD∽△ACD.

【解析】

（1）要使∠ACB是直角，根据圆周角定理可知AB为直径，故圆心O在AB上；（2）要使△ABC∽△CBD∽△ACD，则需要∠ABC=∠ACD，则可得到CD⊥AB.

（1）如图，要使∠ACB是直角，

可知AB为直径，

故圆心O在AB上；

（2）如图，要使△ABC∽△CBD∽△ACD，则需要∠ABC=∠ACD，

又∠ACD+∠BCD=90°，

∴∠B+∠BCD=90°

则CD⊥AB.

练习册系列答案
相关题目

【题目】已知二次函数y＝﹣x2+2mx﹣m2+4．

（1）求证：该二次函数的图象与x轴必有两个交点；

（2）若该二次函数的图象与x轴交于点A、B（点A在点B的左侧），顶点为C，

①求△ABC的面积；

②若点P为该二次函数图象上位于A、C之间的一点，则△PAC面积的最大值为　 　，此时点P的坐标为　 　．

【题目】如图，在△ABC 中，AB=4，D 是 AB 上的一点（不与点 A、B 重合），DE∥BC，交AC 于点 E.设△ABC 的面积为 S，△DEC 的面积为 S'.

（1）当D是AB中点时，求的值；
（2）设AD=x，=y，求y与x的函数表达式，并写出自变量x的取值范围；
（3）根据y的范围，求S-4S′的最小值．

【题目】如图，△ABC的外接圆圆心O在AB上，点D是BC延长线上一点，DM⊥AB于M，交AC于N，且AC=CD．CP是△CDN的边ND上的中线．

(1)求证：AB=DN；

(2)试判断CP与⊙O的位置关系，并证明你的结论；

(3)若PC＝5，CD＝8，求线段MN的长．

【题目】某水果店以4元/千克的价格购进一批水果，由于销售状况良好，该店又再次购进同一种水果，第二次进货价格比第一次每千克便宜了0.5元，所购水果重量恰好是第一次购进水果重量的2倍，这样该水果店两次购进水果共花去了2200元.

(1)该水果店两次分别购买了多少元的水果?

(2)在销售中，尽管两次进货的价格不同，但水果店仍以相同的价格售出，若第一次购进的水果有3%的损耗，第二次购进的水果有5%的损耗，该水果店希望售完这些水果获利不低于1244元，则该水果每千克售价至少为多少元?

【题目】如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM=b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD=∠AND；②△ABM≌△NGF；③CP=；④；其中正确的个数是( )

A. 1B. 2C. 3D. 4

【题目】从三角形不是等腰三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

如图1，在中，CD为角平分线，，，求证：CD为的完美分割线．

在中，，CD是的完美分割线，且为等腰三角形，求的度数．

如图2，中，，，CD是的完美分割线，且是以CD为底边的等腰三角形，求完美分割线CD的长．

【题目】已知：如图，BC为⊙O的弦，点A为⊙O上一个动点，△OBC的周长为16．过C作CD∥AB交⊙O于D，BD与AC相交于点P，过点P作PQ∥AB交于Q，设∠A的度数为α．

（1）如图1，求∠COB的度数（用含α的式子表示）；

（2）如图2，若∠ABC＝90°时，AB＝8，求阴影部分面积（用含α的式子表示）；

（3）如图1，当PQ＝2，求的值．

【题目】已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C。

（1）如图①，若AB＝2，∠P＝30°，求AP的长（结果保留根号）；

（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网