جâؤ؟ؤعبف
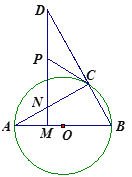
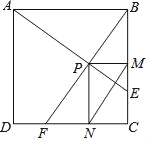
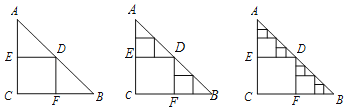
،¾جâؤ؟،؟،÷ABCتاز»صإµبرüض±½اب½اذخض½°ه£¬،دC£½90،م£¬AC£½BC£½2£¬شعصâصإض½°هضذ¼ô³ِز»¸ِ¾،؟ةؤـ´َµؤص·½ذخ³ئخھµع1´خ¼ôب،£¬¼اثùµأص·½ذخأو»خھS1£¨بçح¼1£©£»شعسàدآµؤRt،÷ADE؛حRt،÷BDFضذ£¬·ض±ً¼ôب،ز»¸ِ¾،؟ةؤـ´َµؤص·½ذخ£¬µأµ½ء½¸ِدàح¬µؤص·½ذخ£¬³ئخھµع2´خ¼ôب،£¬²¢¼اصâء½¸ِص·½ذخأو»؛حخھS2£¨بçح¼2£©£»¼جذّ²ظ×÷دآب¥،£»µع2019´خ¼ôب،؛َ£¬سàدآµؤثùسذذ،ب½اذخµؤأو»ض®؛حتا_____£®
،¾´ً°¸،؟![]()
،¾½âخِ،؟
¸ù¾فجâز⣬؟ةاَµأS،÷AED+S،÷DBF£½Sص·½ذخECFD£½S1£½1£¬ح¬ہي؟ةµأ¹وآة£؛Sn¼´تاµعn´خ¼ôب،؛َت£سàب½اذخأو»؛ح£¬¸ù¾ف´ث¹وآةاَ½â¼´؟ة´ً°¸£®
،كثؤ±كذخECFDتاص·½ذخ£¬
،àDE£½EC£½CF£½DF£¬،دAED£½،دDFB£½90،م£¬
،ك،÷ABCتاµبرüض±½اب½اذخ£¬
،à،دA£½،دB£½45،م£¬
،àAE£½DE£½EC£½DF£½BF£½EC£½CF£¬
،كAC£½BC£½2£¬
،àDE£½DF£½1£¬
،àS،÷AED+S،÷DBF£½Sص·½ذخECFD£½S1£½1£»
ح¬ہي£؛S2¼´تاµع¶´خ¼ôب،؛َت£سàب½اذخأو»؛ح£¬
Sn¼´تاµعn´خ¼ôب،؛َت£سàب½اذخأو»؛ح£¬
،àµعز»´خ¼ôب،؛َت£سàب½اذخأو»؛حخھ£؛2©پS1£½1£½S1£¬
µع¶´خ¼ôب،؛َت£سàب½اذخأو»؛حخھ£؛S1©پS2£½1©پ![]() £½
£½![]() £½S2£¬
£½S2£¬
µعب´خ¼ôب،؛َت£سàب½اذخأو»؛حخھ£؛S2©پS3£½![]() ©پ
©پ![]() £½
£½![]() £½S3£¬
£½S3£¬
،
µعn´خ¼ôب،؛َت£سàب½اذخأو»؛حخھ£؛Sn©پ1©پSn£½Sn£½![]() £®شٍs2019£½
£®شٍs2019£½![]() £»
£»
¹ت´ً°¸خھ£؛![]() £®
£®

 ±¸ص½ضذ؟¼؛®¼ظدµءذ´ً°¸
±¸ص½ضذ؟¼؛®¼ظدµءذ´ً°¸