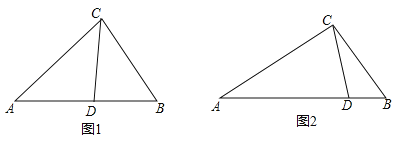题目内容
【题目】如图,已知∠MON,点A在射线OM上.根据下列方法画图.
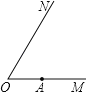
①以O为圆心,OA长为半径画圆,交ON于点B,交射线OM的反向延长线于点C,连接BC;
②以OA为边,在∠MON的内部,画∠AOP=∠OCB;
③连接AB,交OP于点E;
④过点A作⊙O的切线,交OP于点F.
(1)依题意补全图形;
(2)求证∠MOP=∠PON;
(3)若∠MON=60°,OF=10,求AE的长.
【答案】(1)如图所示,见解析;(2)见解析;(3)AE=![]() .
.
【解析】
(1)题干要求根据下列方法画图,根据题意用尺规补全图形即可.
(2)题干要求证∠MOP=∠PON,根据圆周角定理知道∠MON=2∠OCB,从而进行分析证明即可.
(3)根据FA是⊙O的切线,可以知道FA⊥OA,∠MON=60°,利用锐角三角函数可以求知OA=OB,进而求知∠MOP=∠PON,求出AE的长.
解:(1)如图所示:
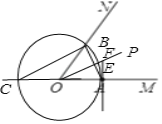
(2)∵∠MON=2∠OCB,
∵∠AOP=∠OCB,
∴∠BOP=∠OCB=∠AOP,
即∠MOP=∠PON;
(3)∵∠MON=60°,
∴∠AOP=30°,
∵FA是⊙O的切线,
∴FA⊥OA,
∵OF=10,
∴OA=5![]() ,
,
∵OA=OB,
∴△OAB是等边三角形,
∵∠MOP=∠PON,
∴OE⊥AB,
∴AE=![]() .
.

练习册系列答案
相关题目
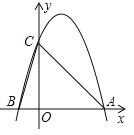
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y=ax2+bx+c | … | t | m | ﹣2 | ﹣2 | n | … |
且当x=﹣![]() 时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<
时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<![]() ,其中,正确结论的是( )
,其中,正确结论的是( )
A.①②③B.①②C.①③D.②③