Question

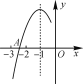
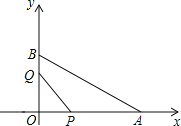
【题目】如图，在平面直角坐标系中，已知OA=12cm，OB=6cm.点P从点O开始沿0A边向点A以1cm/s的速度移动；点Q从点B开始沿BO边向点O以1cm/s的速度移动，如果点P、Q同时出发，用t(s)表示移动的时间(0≤t<6)，那么:

(1)设ΔPOQ的面积为y，求y关于t的函数关系式；

(2)当ΔPOQ的面积为4.5cm时，ΔPOQ沿直线PQ翻折后得到ΔPCQ.试判断点C是否落在直线AB上，并说明理由；

(3)当t为何值时，△POQ与△AOB相似.

Answer 1

【答案】（1）；（2）点C不在直线AB上；（3）t=2或t=4

【解析】

（1）根据S△POQ= POOQ，再把OQ=6-t，OP=t代入整理即可；

（2）令，求出t，即可求出OP=3，OQ=3，即可知△POQ是等腰直角三角形，根据折叠的性质知点C的坐标是(3，3)，求出直线AB的函数关系式，把点C代入函数解析式即可得出点C不在直线AB上；

（3）分两种情形讨论即可①若△POQ∽△AOB时，得 ，②若△POQ∽△BOA时，得 ，分别解方程即可．

(1)∵OQ=6-t

∴

(2)当△POQ的面积为4.5cm时，即

∴t=3

易得△POQ是等腰直角三角形

∴点C的坐标是(3，3)

而直线AB的函数关系式是

当时，

∴点C不在直线AB上

（3）∵OB=6cm，点P从O点开始沿OA边向点A以1cm/s的速度移动，
∴OQ=（6-t）cm，
∵点Q从点B开始沿BO边向点O以1cm/s的速度移动，
∴OP=t（cm），
若△POQ∽△AOB时，

得 即

整理得：12-2t=t，
解得：t=4，
则当t=4时，△POQ与△AOB相似；
若△POQ∽△BOA时，

得 ，

即

解得：t=2，
则当t=2时，△POQ与△BOA相似；
综上所述：当t=4s或2s时，△POQ与△AOB相似.