Question

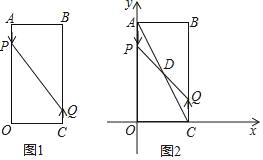
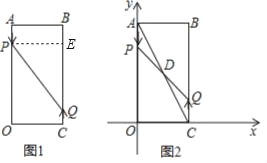
【题目】如图1，已知矩形AOCB，AB=6cm，BC=16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动．

（1）当运动时间为2s时，P、Q两点的距离为　 　cm；

（2）请你计算出发多久时，点P和点Q之间的距离是10cm；

（3）如图2，以点O为坐标原点，OC所在直线为x轴，OA所在直线为y轴，1cm长为单位长度建立平面直角坐标系，连结AC，与PQ相交于点D，若双曲线过点D，问k的值是否会变化？若会变化，说明理由；若不会变化，请求出k的值．

Answer 1

【答案】（1）6；（2）t=或t=，理由见解析；（3）k的值是不会变化，k= ,理由见解析

【解析】

（1）构造出直角三角形，再求出PE，QE，利用勾股定理即可得出结论；

（2）同（2）的方法利用勾股定理建立方程求解即可得出结论；

（3）先求出直线AC解析式，再求出点P，Q坐标，进而求出直线PQ解析式，联立两解析式即可得出结论．

（1）如图1，由运动知，AP=3×2=6cm，CQ=2×2=4cm，

过点P作PE⊥BC于E，过点Q作QF⊥OA于F，

∴四边形APEB是矩形，

∴PE=AB=6，BE=6，

∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6，

根据勾股定理得，PQ=6，

故答案为6；

（2）设运动时间为t秒时，

由运动知，AP=3t，CQ=2t，

同（2）的方法得，PE=6，EQ=16﹣3t﹣2t=16﹣5t，

∵点P和点Q之间的距离是10cm，

∴62+（16﹣5t）2=100，

∴t=或t=；

（3）k的值是不会变化，

理由：∵四边形AOCB是矩形，

∴OC=AB=6，OA=16，

∴C（6，0），A（0，16），

设AC直线为y=kx+b，

把C（6，0），A（0，16）代入得，解得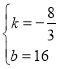

∴直线AC的解析式为y=﹣x+16①，

设运动时间为t，

∴AP=3t，CQ=2t，

∴OP=16﹣3t，

∴P（0，16﹣3t），Q（6，2t），

设PQ直线为y=kx+b，

把P（0，16﹣3t），Q（6，2t），代入得，解得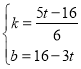

∴PQ解析式为y=x+16﹣3t②，

联立①②解得，x=，y=，

∴D（，），

∴k=×=是定值．