题目内容
【题目】二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y＝ax2+bx+c | … | t | m | ﹣2 | ﹣2 | n | … |
且当x＝﹣
时，与其对应的函数值y＞0，有下列结论：①函数图象的顶点在第四象限内；②﹣2和3是关于x的方程ax2+bx+c＝t的两个根；③0＜m+n＜
，其中，正确结论的是（ ）
A.①②③B.①②C.①③D.②③
【答案】B
【解析】
根据图表信息可知图象过点（0，﹣2），（1，﹣2），依据对称轴以及与系数的关系分析即可.
解：①根据图表可知：
二次函数y＝ax2+bx+c的图象过点（0，﹣2），（1，﹣2），
∴对称轴为直线x＝
＝
，c＝﹣2，
∴a＞0，b＜0，
∴函数图象的顶点在第四象限内；
∴①正确；
②根据二次函数的对称性可知：
（﹣2，t）关于对称轴x＝的对称点为（3，t），
即﹣2和3是关于x的方程ax2+bx+c＝t的两个根，
∴②正确；
③∵对称轴为直线x＝
∴﹣
＝，
∴b＝﹣a，
∵当x＝﹣时，与其对应的函数值y＞0，
∴
a﹣b﹣2＞0，即a+﹣2＞0，∴a＞
．
∵对称轴为直线x＝，二次函数y＝ax2+bx+c的图象过点（﹣1，m）（2，n），
∴m＝n，当x＝﹣1时，m＝a﹣b+c＝a+a﹣2＝2a﹣2，
∴m+n＝4a﹣4，∵a＞．
∴4a﹣4
，
∴③错误．
故选：B．
小学课时特训系列答案
【题目】参照学习函数的过程方法，探究函数
的图像与性质，因为
，即
，所以我们对比函数
来探究列表：
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点：在平面直角坐标系中以自变量
的取值为横坐标，以
相应的函数值为纵坐标，描出相应的点如图所示：
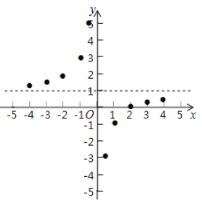
（1）请把
轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当
时，随的增大而______；（“增大”或“减小”）
②的图象是由的图象向______平移______个单位而得到的；
③图象关于点______中心对称.（填点的坐标）
（3）函数与直线
交于点
，
，求
的面积.
