题目内容
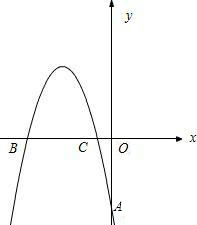
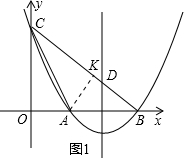
如图,抛物线与x轴交于点A(3,0),B(8,0),与y轴交于点C,且AC平分∠OCB,直线l是它的对称轴.
(1)求直线l和抛物线的解析式;
(2)直线BC与l相交于点D,沿直线l平移直线BC,与直线l,y轴分别交于点E,F,探究四边形CDEF为菱形时点E的坐标;
(3)线段CB上有一动点P,从C点开始以每秒一个单位的速度向B点运动,PM⊥BC,交线段CA于点M,记点P运动时间为t,△CPO与△CPM的面积之差为y,求y与t(0<t≤6)之间的关系式,并确定在运动过程中y的最大值.
(1)求直线l和抛物线的解析式;
(2)直线BC与l相交于点D,沿直线l平移直线BC,与直线l,y轴分别交于点E,F,探究四边形CDEF为菱形时点E的坐标;
(3)线段CB上有一动点P,从C点开始以每秒一个单位的速度向B点运动,PM⊥BC,交线段CA于点M,记点P运动时间为t,△CPO与△CPM的面积之差为y,求y与t(0<t≤6)之间的关系式,并确定在运动过程中y的最大值.

(1)直线l的解析式x=
=
.
如图,过A作AK⊥BC于点K,
∵AC平分∠OCB,
∴AK=OA=3,CK=OC,AB=5,
∴KB=4.
方法一:设OC=x则CB=x+4,由勾股定理得:x2+82=(x+4)2,得x=6,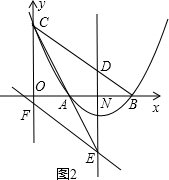
∴C的坐标为(0,6).
方法二:由△ABK∽△CBO得
=
,得OC=6,
∴C的坐标为(0,6)
设抛物线解析式为:y=a(x-3)(x-8),将点C坐标代入可得a=
,
∴所求抛物线解析式为:y=
(x-3)(x-8),
即y=
x2-
x+6.
(2)方法一:
如图,记直线l与x轴交于点N,则NB=2.5,
∵在Rt△OBC中,tanB=
=
,BC=
=10,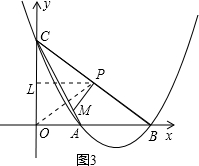
cosB=
,则DN=NB•tanB=
×
=
,
DB=
=
,
∴D点坐标为(
,
).
CD=BC-DB=10-
=
即菱形边长为
.
+
=
,
-
=-5,
∴E点坐标为(
,
)或(
,-5).
方法二:四边形CDEF为菱形时,有两种情况:
①当BC往下平移时,由菱形性质知,点E1即为直线CA与对称轴交点.
求得直线AC方程为:y=-2x+6,
与对称轴x=
的交点为E1(
,-5).
②当BC往上平移时,即D点往上平移菱形的边长个单位得E2.
求得直线BC:y=-
x+6,与对称轴x=
交点D的纵坐标为yD=
,
菱形边长为yD-yE=
-(-5)=
,E2点纵坐标为:
+
=
.
∴四边形CDEF为菱形时,E1(
,-5),E2(
,
).
(3)过点P作PL⊥OC,垂足为L,则∠CPL=∠B,
而Rt△BOC中,sin∠B=
=
,cos∠B=
,
由题意得CP=t,则LP=CPcos∠B=
,
△CPO的面积为:
OC•LP=
t,
∵CA平分∠OCB,
∴∠MCP=∠OCA,
Rt△AOC中,tan∠OCA=
=
,
∴PM=
.
△CPM的面积为:
CP•PM=
t2,
∴y=
t-
t2(0<t≤6),
当t=
时,y有最大值为
.
| 3+8 |
| 2 |
| 11 |
| 2 |
如图,过A作AK⊥BC于点K,
∵AC平分∠OCB,
∴AK=OA=3,CK=OC,AB=5,
∴KB=4.
方法一:设OC=x则CB=x+4,由勾股定理得:x2+82=(x+4)2,得x=6,

∴C的坐标为(0,6).
方法二:由△ABK∽△CBO得
| AK |
| OC |
| KB |
| OB |
∴C的坐标为(0,6)
设抛物线解析式为:y=a(x-3)(x-8),将点C坐标代入可得a=
| 1 |
| 4 |
∴所求抛物线解析式为:y=
| 1 |
| 4 |
即y=
| 1 |
| 4 |
| 11 |
| 4 |
(2)方法一:
如图,记直线l与x轴交于点N,则NB=2.5,
∵在Rt△OBC中,tanB=
| OC |
| OB |
| 3 |
| 4 |
| 62+82 |

cosB=
| 4 |
| 5 |
| 5 |
| 2 |
| 3 |
| 4 |
| 15 |
| 8 |
DB=
| NB |
| cosB |
| 25 |
| 8 |
∴D点坐标为(
| 11 |
| 2 |
| 15 |
| 8 |
CD=BC-DB=10-
| 25 |
| 8 |
| 55 |
| 8 |
| 55 |
| 8 |
| 15 |
| 8 |
| 55 |
| 8 |
| 35 |
| 4 |
| 15 |
| 8 |
| 55 |
| 8 |
∴E点坐标为(
| 11 |
| 2 |
| 35 |
| 4 |
| 11 |
| 2 |
方法二:四边形CDEF为菱形时,有两种情况:
①当BC往下平移时,由菱形性质知,点E1即为直线CA与对称轴交点.
求得直线AC方程为:y=-2x+6,
与对称轴x=
| 11 |
| 2 |
| 11 |
| 2 |
②当BC往上平移时,即D点往上平移菱形的边长个单位得E2.
求得直线BC:y=-
| 3 |
| 4 |
| 11 |
| 2 |
| 15 |
| 8 |
菱形边长为yD-yE=
| 15 |
| 8 |
| 55 |
| 8 |
| 15 |
| 8 |
| 55 |
| 8 |
| 35 |
| 4 |
∴四边形CDEF为菱形时,E1(
| 11 |
| 2 |
| 11 |
| 2 |
| 35 |
| 4 |
(3)过点P作PL⊥OC,垂足为L,则∠CPL=∠B,
而Rt△BOC中,sin∠B=
| OC |
| BC |
| 3 |
| 5 |
| 4 |
| 5 |
由题意得CP=t,则LP=CPcos∠B=
| 4t |
| 5 |
△CPO的面积为:
| 1 |
| 2 |
| 12 |
| 5 |
∵CA平分∠OCB,
∴∠MCP=∠OCA,
Rt△AOC中,tan∠OCA=
| OA |
| OC |
| 1 |
| 2 |
∴PM=
| t |
| 2 |
△CPM的面积为:
| 1 |
| 2 |
| 1 |
| 4 |
∴y=
| 12 |
| 5 |
| 1 |
| 4 |
当t=
| 24 |
| 5 |
| 144 |
| 25 |


练习册系列答案
相关题目

 、B两点.
、B两点.