题目内容
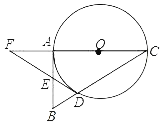
【题目】如图，在⊙O中，弦AB=1，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为___．
【答案】
【解析】
作OH⊥AB，延长DC交⊙O于E，如图，根据垂径定理得到AH=BH=AB=，CD=CE，再判断出△BCD∽△ECA得出CDCE=BCAC，易得CD=
，当CH最小时，CD最大，C点运动到H点时，CH最小，所以CD的最大值为．
解：作OH⊥AB，延长DC交⊙O于E，如图，
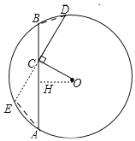
∴AH=BH=AB=，
∵CD⊥OC，
∴CD=CE，
∵∠ABD=∠DEA，∠BCD=∠ECA，
∴△BCD∽△ECA，
∴
，
∴CDCE=BCAC，
∴CD2=（BH-CH）（AH+CH）=（-CH）（+CH）=
-CH2，
∴CD=，
∴当CH最小时，CD最大，
而C点运动到H点时，CH最小，
此时CD=，即CD的最大值为．
故答案为．
阅读快车系列答案
【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项，每4年评选一次，在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家，美籍华人丘成桐1982年获得费尔兹奖．为了让学生了解费尔兹奖得主的年龄情况，我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据，并对数据进行整理、描述和分析．下面给出了部分信息．
a．截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1（数据分成5组，各组是28≤x＜31，31≤x＜34，34≤x＜37，37≤x＜40，x≥40）：
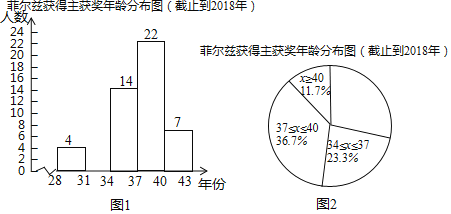
b．如图2，在a的基础上，画出扇形统计图；
c．截止到2018年费尔兹奖得主获奖时的年龄在34≤x＜37这一组的数据是：
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d．截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下：
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37，38 |
根据以上信息，回答下列问题：
（1）依据题意，补全频数直方图；
（2）31≤x＜34这组的圆心角度数是度，并补全扇形统计图；
（3）统计表中中位数m的值是；
（4）根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征．
【题目】某农作物的生长率P与温度t(℃)有如下关系：如图1，当10≤t≤25时可近似用函数
刻画；当25≤t≤37时可近似用函数
刻画．
(1)求h的值．
(2)按照经验，该作物提前上市的天数m(天)与生长率P满足函数关系：
生长率P | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m（天） | 0 | 5 | 10 | 15 |
①请运用已学的知识，求m关于P的函数表达式；
②请用含
的代数式表示m ；
(3)天气寒冷，大棚加温可改变农作物生长速度．在(2)的条件下，原计划大棚恒温20℃时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出(一次售完)，销售额可增加600元．因此给大棚继续加温，加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．
