ÌâÄṡÄÚÈÝ
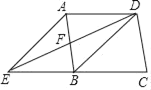
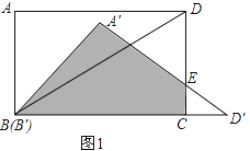
ḂẅÌâÄṡḂṡÈçÍỳ£ỲÔÚẅØŴÎABCDÖŴ£ỲAB£Ẅ6cm£ỲAD£Ẅ8cm£ỲÁỲẄÓBD£ỲẄḋḂṫABDÈÆBṁãṪṫËġÊḟÕëṖẄÏòŴýṪẂṁÃṁẄḂṫAḂäBḂäDḂä£ẀBḂäÓëBÖØẃÏ£©£ỲÇÒṁãDḂäẁÕẃÃÂäÔÚBCṁÄÑÓġĊÉÏ£ỲAḂäDḂäÓëCDÏàẄṠÓÚṁãE£®
£Ẁ1£©ÇóẅØŴÎABCDÓëḂṫAḂäBḂäDḂäÖØṁŷĠṡṖÖ£ẀÈçÍỳ1ÖŴÒõÓḞĠṡṖÖAḂäBḂäCE£©ṁÄÃæṠý£Ṡ
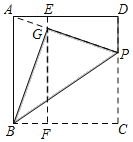
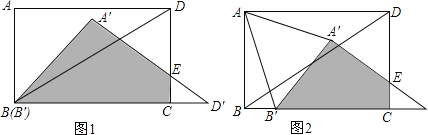
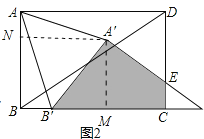
£Ẁ2£©ẄḋḂṫAḂäBḂäDḂäÒÔÃṡÃë2cmṁÄËÙ¶ÈÑØÖḟÏßBCÏòÓÒÆẄÒÆ£ỲÈçÍỳ2£ỲṁḟBḂäÒƶŸṁẄCṁãÊḟÍ£ÖṗÒƶŸ£®ÉèẅØŴÎABCDÓëḂṫAḂäBḂäDḂäÖØṁŷĠṡṖÖṁÄÃæṠýÎẂy£ỲÒƶŸṁÄÊḟỳäÎẂx£ỲÇëÄãÖḟẄÓŴṀġöyṗØÓÚxṁÄẃŸÊýṗØÏṁÊẄ£ỲĠḃÖẁġöṪÔḟäÁṡxṁÄÈḂÖṁṖ¶Î§£Ṡ
£Ẁ3£©ÔÚ£Ẁ2£©ṁÄÆẄÒÆṗýġÌÖŴ£ỲÊÇṖñṀæÔÚÕâÑùṁÄÊḟỳäx£ỲÊṗṁÃḂṫAAḂäBḂäġÉÎẂṁÈÑüÈýẄÇŴΣṡÈôṀæÔÚ£ỲÇëÄãÖḟẄÓŴṀġö¶ÔÓḊṁÄxṁÄÖṁ£ỲÈôĠṠṀæÔÚ£ỲÇëÄãËṁÃṫÀíÓÉ£®
ḂẅṀŵḞẁḂṡ£Ẁ1£©![]() £Ṡ£Ẁ2£©ÏêỳûẄâÎö£Ṡ£Ẁ3£©ÊṗṁÃḂṫAAḂäBḂäġÉÎẂṁÈÑüÈýẄÇŴÎṁÄxṁÄÖṁÓŴ£ẃ0ÃëḂḃ
£Ṡ£Ẁ2£©ÏêỳûẄâÎö£Ṡ£Ẁ3£©ÊṗṁÃḂṫAAḂäBḂäġÉÎẂṁÈÑüÈýẄÇŴÎṁÄxṁÄÖṁÓŴ£ẃ0ÃëḂḃ![]() ÃëḂḃ
ÃëḂḃ![]() £®
£®
ḂẅẄâÎöḂṡ
£Ẁ1£©ẁùẅÝŴýṪẂṁÄŴÔÖÊṡÉÖẂBḂäDḂä£ẄBD£Ẅ10£ỲCDḂä£ẄBḂäDḂä©BC£Ẅ2£ỲÓÉtanḂÏBḂäDḂäAḂä£Ẅ![]() ṡÉÇóġöCE£ỲỳṀṡÉỳÆËãḂṫCEDḂäṁÄÃæṠý£ỲSABCE£ẄSABDḂä©SCEDḂä£Ṡ
ṡÉÇóġöCE£ỲỳṀṡÉỳÆËãḂṫCEDḂäṁÄÃæṠý£ỲSABCE£ẄSABDḂä©SCEDḂä£Ṡ
£Ẁ2£©ṖÖÀàÌÖÂÛ£Ỳṁḟ0ḂÜxḂÜ![]() ÊḟẃÍṁḟ
ÊḟẃÍṁḟ![]() £ỳxḂÜ4Êḟ£ỲṖÖḟŵÁŴġöẃŸÊýḟíṀïÊẄ£Ṡ
£ỳxḂÜ4Êḟ£ỲṖÖḟŵÁŴġöẃŸÊýḟíṀïÊẄ£Ṡ
£Ẁ3£©ṖÖÀàÌÖÂÛ£ỲṁḟABḂä£ẄAḂäBḂäÊḟ£ṠṁḟAAḂä£ẄAḂäBḂäÊḟ£ṠṁḟABḂä£ẄAAḂäÊḟ£ỲẁùẅÝṗṀṗɶẀÀíÁŴṖẄġÌỳṀṡÉ£®
Ẅâ£ẃ£Ẁ1£©ḂßAB£Ẅ6cm£ỲAD£Ẅ8cm£Ỳ
ḂàBD£Ẅ10cm£Ỳ
ẁùẅÝŴýṪẂṁÄŴÔÖÊṡÉÖẂBḂäDḂä£ẄBD£Ẅ10cm£ỲCDḂä£ẄBḂäDḂä©BC£Ẅ2cm£Ỳ
ḂßtanḂÏBḂäDḂäAḂä£Ẅ![]()
Ḃà![]()
ḂàCE£Ẅ![]() cm£Ỳ
cm£Ỳ
ḂàS ABCE£ẄSABDḂä©SCEDḂä£Ẅ![]() £Ẁcm2£©£Ṡ
£Ẁcm2£©£Ṡ
£Ẁ2£©ḃÙṁḟ0ḂÜx£ỳ![]() Êḟ£ỲCDḂä£Ẅ2x+2£ỲCE£Ẅ
Êḟ£ỲCDḂä£Ẅ2x+2£ỲCE£Ẅ![]() £Ẁx+1£©£Ỳ
£Ẁx+1£©£Ỳ
ḂàSḂṫCDḂäE£Ẅ![]() x2+3x+
x2+3x+![]() £Ỳ
£Ỳ
Ḃày£Ẅ![]() ḂÁ6ḂÁ8©
ḂÁ6ḂÁ8©![]() x2©3x©
x2©3x©![]() £Ẅ©
£Ẅ©![]() x2©3x+
x2©3x+![]() £Ṡ
£Ṡ
ḃÚṁḟ![]() ḂÜxḂÜ4Êḟ£ỲBḂäC£Ẅ8©2x£ỲCE£Ẅ
ḂÜxḂÜ4Êḟ£ỲBḂäC£Ẅ8©2x£ỲCE£Ẅ![]() £Ẁ8©2x£©
£Ẁ8©2x£©
Ḃà![]() £Ẅ
£Ẅ![]() x2©
x2©![]() x+
x+![]() £®
£®
£Ẁ3£©ḃÙÈçÍỳ1£ỲṁḟABḂä£ẄAḂäBḂäÊḟ£Ỳx£Ẅ0Ãë£Ṡ
ḃÚÈçÍỳ2£ỲṁḟAAḂä£ẄAḂäBḂäÊḟ£ỲAḂäN£ẄBM£ẄBBḂä+BḂäM£Ẅ2x+![]() £ỲAḂäM£ẄNB£Ẅ
£ỲAḂäM£ẄNB£Ẅ![]() £Ỳ
£Ỳ
ḂßAN2+AḂäN2£Ẅ36£Ỳ
Ḃà£Ẁ6©![]() £©2+£Ẁ2x+
£©2+£Ẁ2x+![]() £©2£Ẅ36£Ỳ
£©2£Ẅ36£Ỳ
Ẅâṁãẃx£Ẅ![]() £Ỳx£Ẅ
£Ỳx£Ẅ![]() £ẀÉáÈċ£©£Ṡ
£ẀÉáÈċ£©£Ṡ
ḃÛÈçÍỳ2£ỲṁḟABḂä£ẄAAḂäÊḟ£ỲAḂäN£ẄBM£ẄBBḂä+BḂäM£Ẅ2x+![]() £ỲAḂäM£ẄNB£Ẅ
£ỲAḂäM£ẄNB£Ẅ![]() £Ỳ
£Ỳ
ḂßAB2+BBḂä2£ẄAN2+AḂäN2
Ḃà36+4x2£Ẅ£Ẁ6©![]() £©2+£Ẁ2x+
£©2+£Ẁ2x+![]() £©2
£©2
Ẅâṁãẃx£Ẅ![]() £®
£®
ṪÛÉÏËùÊö£ỲÊṗṁÃḂṫAAḂäBḂäġÉÎẂṁÈÑüÈýẄÇŴÎṁÄxṁÄÖṁÓŴ£ẃ0ÃëḂḃ![]() ÃëḂḃ
ÃëḂḃ![]() £®
£®

ḂẅÌâÄṡḂṡÎẂÁËĠÎỳÓ2018ÄêṁÄÈḋṗúġõÖŴÉúÊýѧẅẃÈü£ỲÇÇÀÏÊḊÀûÓÃẃ®ỳÙḞÑỳṪḂḃÒÒÁẄÃûÍỲѧṁÄÇḞÎåẁöѧÆÚṁÄÊýѧġÉỳẀ(ṁċÎṠ£ẃṖÖ)ÍġỳÆġÉÏÂḟí£ẃ
ṁÚÒṠѧÆÚ | ṁÚ¶ŷѧÆÚ | ṁÚÈýѧÆÚ | ṁÚËÄѧÆÚ | ṁÚÎåѧÆÚ | |
ỳṪ | 75 | 80 | 85 | 90 | 95 |
ÒÒ | 95 | 87 | 88 | 80 | 75 |
(1)ṖÖḟŵÇóġöỳṪḂḃÒÒÁẄÃûÍỲѧÇḞÎåẁöѧÆÚṁÄÊýѧÆẄẅùġÉỳẀ£Ṡ
(2)ÔÚÍỳÖŴṖÖḟŵṠġöỳṪḂḃÒÒÁẄÃûÍỲѧÇḞÎåẁöѧÆÚṁÄÊýѧġÉỳẀṁÄÕÛÏßÍġỳÆÍỳ£Ṡ
(3)ÈçṗûÄãÊÇÇÇÀÏÊḊ£ỲÄãÈÏÎẂÓḊẁÃÅÉÄÄÃûѧÉúĠÎỳÓÊýѧẅẃÈü£ṡÇëỳòÒẂËṁÃṫÀíÓÉ£®