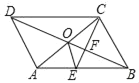
题目内容
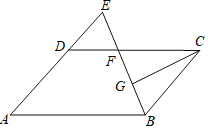
【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②SABCD=ACBC;③OE:AC=![]() :6; ④SOEF=
:6; ④SOEF=![]() SABCD,成立的是_____.
SABCD,成立的是_____.
【答案】①②③
【解析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到SABCD=ACBC,故②正确,根据直角三角形的性质得到AC=![]() BC,根据三角形的中位线的性质得到OE=
BC,根据三角形的中位线的性质得到OE=![]() BC,于是得到OE:AC=
BC,于是得到OE:AC=![]() :6;故③正确;根据相似三角形的性质得到
:6;故③正确;根据相似三角形的性质得到![]() =
=![]() =2,求得S△OCF=2S△OEF,所以S△OEF=
=2,求得S△OCF=2S△OEF,所以S△OEF=![]() S△OEC,又因为OE=
S△OEC,又因为OE=![]() BC=
BC=![]() AD,S△OEC= S△OEB,所以S△OEC= S△OEB=
AD,S△OEC= S△OEB,所以S△OEC= S△OEB=![]() S△ABD=
S△ABD=![]() S ABCD,可得:S△OEF=
S ABCD,可得:S△OEF=![]() ×
×![]() S ABCD=
S ABCD=![]() ,故④不正确.
,故④不正确.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
∵AC⊥BC,
∴SABCD=ACBC,故②正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=![]() BC,
BC,
∵AO=OC,AE=BE,
∴OE=![]() BC,
BC,
∴OE:AC=![]() BC:
BC:![]() BC,
BC,
∴OE:AC=![]() :6;故③正确;
:6;故③正确;
∵AO=OC,AE=BE,
∴OE∥BC,
∴△OEF∽△BCF,![]() =
=![]() =2:1 ,
=2:1 ,
∴S△OCF:S△OEF=![]() =2,
=2,
∴S△OCF=2S△OEF,
∴S△OEF=![]() S△OEC,
S△OEC,
又∵OE=![]() BC=
BC=![]() AD,S△OEC= S△OEB,
AD,S△OEC= S△OEB,
∴ S△OEC= S△OEB=![]() S△ABD=
S△ABD=![]() S ABCD,
S ABCD,
即S△OEF=![]() ×
×![]() S ABCD=
S ABCD=![]() ,
,
故④不正确.
故答案为:①②③.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案