Question

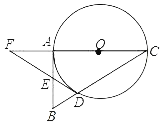
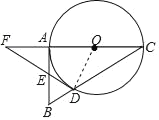
【题目】如图，在△ABC中，∠BAC＝90°，以AC为直径的⊙O交BC于点D，点E在AB上，连接DE并延长交CA的延长线于点F，且∠AEF＝2∠C．

（1）判断直线FD与⊙O的位置关系，并说明理由；

（2）若AE＝2，EF＝4，求⊙O的半径．

Answer 1

【答案】（1）直线FD与⊙O相切，理由详见解析；（2）⊙O的半径为2．

【解析】

（1）连接OD，根据已知条件得到∠AEF＝∠AOD，等量代换得到∠AOD＋∠AED＝180°，求得∠ODF＝90°，于是得到结论；

（2）解直角三角形得到∠F＝30°，AF＝，求得OF＝2OD，于是得到OD＝FA，即可得到结论．

解：（1）直线FD与⊙O相切；

理由：连接OD，

∵∠AEF＝2∠C，∠AOD＝2∠C，

∴∠AEF＝∠AOD，

∵∠AEF+∠AED＝180°，

∴∠AOD+∠AED＝180°，

∵∠BAC＝90°，

∴∠ODF＝90°，

∴直线FD与⊙O相切；

（2）∵∠BAC＝90°，AE＝2，EF＝4，

∴∠F＝30°，AF＝，

∵∠ODF＝90°，

∴OF＝2OD，

∴OD＝FA，

∴⊙O的半径为．