题目内容
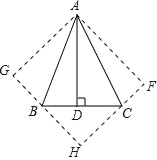
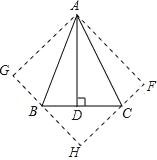
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
(1)求证:四边形AFHG为正方形;
(2)若BD=6,CD=4,求AB的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)由折叠的性质可得到的条件是:①AG=AD=AF,②∠GAF=∠GAD+∠DAF=2∠BAC=90°,且∠G=∠F=90°;由②可判定四边形AGHF是矩形,由AG=AF可证得四边形AGHF是正方形;
(2)设AD=x,由折叠的性质可得:AD=AF=x(即正方形的边长为x),BG=BD=6,CF=CD=4;进而可用x表示出BH、HC的长,即可在Rt△BHC中,由勾股定理求得AD的长,进而可求出AB的长.
试题解析:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°;
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°;
∴∠GAF=∠BAG+∠CAF+∠BAC=90°;
∴四边形AFHG是正方形;
(2)∵四边形AFHG是正方形,
∴∠BHC=90°,
又GH=HF=AD,GB=BD=6,CF=CD=4,
设AD的长为x,则BH=GH﹣GB=x﹣6,CH=HF﹣CF=x﹣4,
在Rt△BCH中,BH2+CH2=BC2,
∴(x﹣6)2+(x﹣4)2=102,
解得x1=12,x2=﹣2(不合题意,舍去),
∴AD=12,
∴AB=![]() .
.

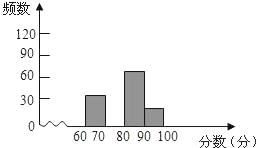
【题目】为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m= ,n= ;
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段;
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?