题目内容
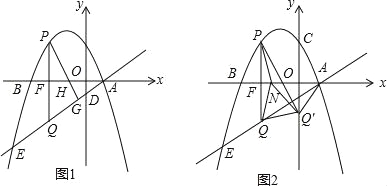
【题目】如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A、B两点(点A在点B的右侧),交y轴于点C,点D的坐标为(0,﹣1),直线AD交抛物线于另一点E,点P是第二象限抛物线上的一点,作PQ∥y轴交直线AE于Q,作PG⊥AD于G,交x轴于点H
x+3与x轴交于A、B两点(点A在点B的右侧),交y轴于点C,点D的坐标为(0,﹣1),直线AD交抛物线于另一点E,点P是第二象限抛物线上的一点,作PQ∥y轴交直线AE于Q,作PG⊥AD于G,交x轴于点H
(1)求线段DE的长;
(2)设d=PQ﹣![]() PH,当d的值最大时,在直线AD上找一点K,使PK+
PH,当d的值最大时,在直线AD上找一点K,使PK+![]() EK的值最小,求出点K的坐标和PK+
EK的值最小,求出点K的坐标和PK+![]() EK的最小值;
EK的最小值;
(3)如图2,当d的值最大时,在x轴上取一点N,连接PN,QN,将△PNQ沿着PN翻折,点Q的对应点为Q′,在x轴上是否存在点N,使△AQQ′是等腰三角形?若存在,求出点N的坐标,若不存在,说明理由.
【答案】(1)8.(2)K(﹣2![]() ,﹣3),最小值为8.(3)满足条件的点N坐标为(6﹣5
,﹣3),最小值为8.(3)满足条件的点N坐标为(6﹣5![]() ,0)或(
,0)或(![]() ,0)或(﹣3
,0)或(﹣3![]() ,0)或(﹣6﹣5
,0)或(﹣6﹣5![]() ,0).
,0).
【解析】
试题分析:(1)先求出点A坐标,求出直线AD的解析式,利用方程组求出点E坐标,利用两点间距离公式即可解决问题.
(2)构建二次函数,求出d最大时点P坐标,作EM⊥PQ交PQ的延长线于M,作KN⊥EM于N.只要证明PM就是PK+![]() EK的最小值即可解决问题.
EK的最小值即可解决问题.
(3)分四种情形①如图2中,当Q′Q=AQ′时,∠Q′PQ=∠Q′PA=30°,∠NPE=∠NPQ′=15°,连接PA,在PF上取一点E,使得PE=EN.设FN=x,则PE=EN=2x,EF=![]() x,列出方程求解即可.②如图3中,当N与A重合时△AQQ′是等腰三角形.此时N(
x,列出方程求解即可.②如图3中,当N与A重合时△AQQ′是等腰三角形.此时N(![]() ,0).③如图4中,当N与B重合时,△AQQ′是等腰三角形,此时N(﹣3
,0).③如图4中,当N与B重合时,△AQQ′是等腰三角形,此时N(﹣3![]() ,0).④如图5中,当Q′Q=Q′A,易知∠PNF=∠PQQ′=∠PQ′Q=15°,在FN上取一点E,使得PE=BE.在Rt△PEF中解直角三角形即可解决问题.
,0).④如图5中,当Q′Q=Q′A,易知∠PNF=∠PQQ′=∠PQ′Q=15°,在FN上取一点E,使得PE=BE.在Rt△PEF中解直角三角形即可解决问题.
试题解析:(1)对于抛物线y=﹣![]() x2﹣
x2﹣![]() x+3,
x+3,
令y=0,得﹣![]() x2﹣
x2﹣![]() x+3=0,解得x=﹣3
x+3=0,解得x=﹣3![]() 或
或![]() ,∴A(
,∴A(![]() ,0),B(﹣3
,0),B(﹣3![]() ,0),
,0),
∵D(0,﹣1),
设直线AD的解析式为y=kx+b,则有 解得
解得 ,
,
∴直线AD的解析式为y=![]() x﹣1.
x﹣1.
由 解得
解得 或
或 ,∴点E坐标为(﹣4
,∴点E坐标为(﹣4![]() ,﹣5),
,﹣5),
∴DE=![]() =8.
=8.
(2)如图1中,设P(m,﹣![]() m2﹣
m2﹣![]() x+3)则Q(m,
x+3)则Q(m,![]() m﹣1).
m﹣1).

∵tan∠OAD=![]() =
=![]() ,∴∠OAD=30°,∵PG⊥AE,∴∠AGH=90°,∴∠AHG=∠PHF=60°,
,∴∠OAD=30°,∵PG⊥AE,∴∠AGH=90°,∴∠AHG=∠PHF=60°,
∴PH=![]() ,
,
∴d=PQ﹣![]() PH=﹣
PH=﹣![]() m2﹣
m2﹣![]() m+3﹣
m+3﹣![]() ×
×![]() (﹣
(﹣![]() m2﹣
m2﹣![]() m+3)=﹣
m+3)=﹣![]() (m+2
(m+2![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=﹣2![]() 时,d的值最大,P(﹣2
时,d的值最大,P(﹣2![]() ,3),
,3),
作EM⊥PQ交PQ的延长线于M,作KN⊥EM于N.
∵∠AEM=∠OAD=30°,
∴KN=![]() EK,QM=
EK,QM=![]() EQ,
EQ,
∴PK+![]() EK=PK+KN≤PM,
EK=PK+KN≤PM,
∴当K与Q重合时,PK+![]() EK的值最小,
EK的值最小,
此时K(﹣2![]() ,﹣3),最小值为8.
,﹣3),最小值为8.
(3)①如图2中,连接PA,在PF上取一点E,使得PE=EN.

∵PF=3,AF=3![]() ,∴tan∠AFP=
,∴tan∠AFP=![]() ,∴∠PAF=30°,∠PAQ=60°,∵PF=FQ,AF⊥PQ,
,∴∠PAF=30°,∠PAQ=60°,∵PF=FQ,AF⊥PQ,
∴AP=AQ,∴△PAQ是等边三角形,当Q′Q=AQ′时,∠Q′PQ=∠Q′PA=30°,∠NPE=∠NPQ′=15°,
∴∠NEF=30°,设FN=x,则PE=EN=2x,EF=![]() x,∵PF=3,∴2x+
x,∵PF=3,∴2x+![]() x=3,∴x=6﹣3
x=3,∴x=6﹣3![]() ,
,
∴OF=2![]() ﹣6+3
﹣6+3![]() =5
=5![]() ﹣6,∴N(6﹣5
﹣6,∴N(6﹣5![]() ,0).
,0).
②如图3中,当N与A重合时△AQQ′是等腰三角形.此时N(![]() ,0).
,0).

③如图4中,当N与B重合时,△AQQ′是等腰三角形,此时N(﹣3![]() ,0).
,0).

④如图5中,当Q′Q=Q′A,易知∠PNF=∠PQQ′=∠PQ′Q=15°,在FN上取一点E,使得PE=BE.

在Rt△PEF中,∵PF=3,∠PEF=30°,∴PE=NE=2PF=6,EF=![]() PF=3
PF=3![]() ,
,
∴ON=6+5![]() ,∴N(﹣6﹣5
,∴N(﹣6﹣5![]() ,0).
,0).
综上所述,满足条件的点N坐标为(6﹣5![]() ,0)或(
,0)或(![]() ,0)或(﹣3
,0)或(﹣3![]() ,0)或(﹣6﹣5
,0)或(﹣6﹣5![]() ,0).
,0).

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案