题目内容
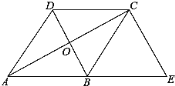
【题目】定义：如图（1），若分别以△ABC的三边AC、BC、AB为边向三角形外侧作正方形ACDE、BCFG和ABMN，则称这三个正方形为△ABC的外展三叶正方形，其中任意两个正方形为△ABC的外展
双叶正方形．
（1）作△ABC的外展双叶正方形ACDE和BCFG，记△ABC，△DCF的面积分别为S1和S2．
①如图（2），当∠ACB=90°时，求证：S1=S2；
②如图（3），当∠ACB≠90°时，S1与S2是否仍然相等，请说明理由．
（2）已知△ABC中，AC=3，BC=4，作其外展三叶正方形，记△DCF、△AEN、△BGM的面积和为S，请利用图（1）探究：当∠ACB的度数发生变化时，S的值是否发生变化？若不变，求出S的值；若变化，求出S的最大值．
【答案】（1）①证明见解析；②S1=S2，理由见解析；（2）S的值发生变化，S的最大值是18.
【解析】分析：（1）由正方形的性质可以得出AC=DC，BC=FC，∠ACB=∠DCF=90°，就可以得出△ABC≌△DFC而得出结论；
（2）如图3，过点A作AP⊥BC于点P，过点D作DQ⊥FC交FC的延长线于点Q，通过证明△APC≌△DQC就有DQ=AP而得出结论；
（3）如图 1，根据（2）可以得出S=3S△ABC，要使S最大，就要使S△ABC最大，当∠AVB=90°时S△ABC最大，就可以求出结论
解析：（1）证明：如图1，∵正方形ACDE和正方形BCFG，
∴AC=DC，BC=FC，∠ACD=∠BCF=90°，
∵∠ACB=90°，∴∠DCF=90°，
∴∠ACB=∠DCF=90°．
在△ABC和△DFC中，
AC＝DC
∠ACB＝∠DCF
BC＝FC
∴△ABC≌△DFC（SAS）．
∴S△ABC=S△DFC，
∴S=S
（2）S1=S2，理由如下：
如图3，过点A作AP⊥BC于点P，过点D作DQ⊥FC交FC的延长线于点Q．
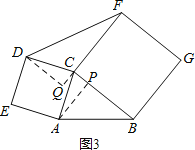
∴∠APC=∠DQC=90°．
∵四边形ACDE，BCFG均为正方形，
∴AC=CD，BC=CF，
∵∠ACP+∠ACQ=90°，∠DCQ+∠ACQ=90°．
∴∠ACP=∠DCQ．
在△APC和△DQC中
∠APC＝∠DQC
∠ACP＝∠DCQ
AC＝DC
∴△APC≌△DQC（AAS），
∴AP=DQ．
∴BC×AP=DQ×FC，
∴S1=S2；
（3）由（2）得，S是△ABC面积的三倍，
要使S最大，只需三角形ABC的面积最大，
∴当△ABC是直角三角形，即∠ACB=90°时，S有最大值．
此时，S=3S△ABC=3×
=18
