��Ŀ����
����Ŀ��������ij��ҵ������Ӧ���������·�չ���ĺ��٣��з���һ���²�Ʒ����֪�з����������ֲ�Ʒ�ijɱ�Ϊ30Ԫ����������������y������������ۼ�x��Ԫ�������ĺ�������ʽΪ��
![]()
��1������ҵ���۸ò�Ʒ����������ΪW����Ԫ������ֱ��д��������W����Ԫ�������ۼ���Ԫ/�����ĺ�������ʽ��
��2�����ò�Ʒ���ۼ�x��Ԫ/����Ϊ����ʱ����ҵ���۸ò�Ʒ��õ����������?����������Ƕ���?
��3������ҵ���۸ò�Ʒ��������������750��Ԫ����ȷ���ò�Ʒ���ۼ�x��Ԫ/������ȡֵ��Χ��
���𰸡���1��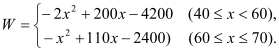 ��2�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ����3��Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55.
��2�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ����3��Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55.
��������
�����������1��������������=����������ÿ����Ʒ������ÿ����Ʒ���ۼ�-ÿ����Ʒ�Ľ��ۣ���ֱ���г�ʽ�ӣ����ɣ���2�����ݶ��κ��������ʣ��ֱ�����������������ֵ���Ƚϼ��ɵý��ۣ���3�����ɣ�2���Ľ��ۣ��ų��ڶ���������ٸ��ݶ��κ��������ʣ��ɵ�һ�����ȷ��x��ȡֵ��Χ.
�����������1��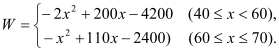
��2������1��֪����540��x<60ʱ��W=-2��x-50��2+800��
��-2<0��������x=50ʱ��W�����ֵ800��
��60��x��70ʱ��W=-��x-55��2+625.
��-1��0�� ����60��x��70ʱ��W��x���������С��
����x=60ʱ��W�����ֵ600��
![]()
�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ��
��3����40��x��60ʱ����W=750����
-2��x-50��2+800=750,��֮����![]()
�ɺ���W=-2��x-50��2+800�����ʿ�֪��
��45��x��55ʱ��W��750��
��60��x��70ʱ��W���ֵΪ600��750.
���ԣ�Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55.

