题目内容
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
【答案】
(1)解:分两种情况
①当1≤x≤20时,将m=25代入m=20+ ![]() x,解得x=10
x,解得x=10
②当21≤x≤30时,25=10+ ![]() ,解得x=28
,解得x=28
经检验x=28是方程的解
∴x=28
答:第10天或第28天时该商品为25元/件.
(2)解:分两种情况
①当1≤x≤20时,y=(m﹣10)n=(20+ ![]() x﹣10)(50﹣x)=﹣
x﹣10)(50﹣x)=﹣ ![]() x2+15x+500,
x2+15x+500,
②当21≤x≤30时,y=(10+ ![]() ﹣10)(50﹣x)=
﹣10)(50﹣x)= ![]()
综上所述: 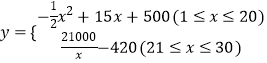
(3)解:①当1≤x≤20时
由y=﹣ ![]() x2+15x+500=﹣
x2+15x+500=﹣ ![]() (x﹣15)2+
(x﹣15)2+ ![]() ,
,
∵a=﹣ ![]() <0,
<0,
∴当x=15时,y最大值= ![]() ,
,
②当21≤x≤30时
由y= ![]() ﹣420,可知y随x的增大而减小
﹣420,可知y随x的增大而减小
∴当x=21时,y最大值= ![]() ﹣420=580元
﹣420=580元
∵ ![]()
∴第15天时获得利润最大,最大利润为612.5元.
【解析】(1)分两种情形分别代入解方程即可.(2)分两种情形写出所获利润y(元)关于x(天)的函数关系式即可.(3)分两种情形根据函数的性质解决问题即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目