题目内容
【题目】如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )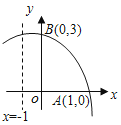
A.顶点坐标为(-1,4)
B.函数的解析式为y=-x2-2x+3
C.当x<0时,y随x的增大而增大
D.抛物线与x轴的另一个交点是(-3,0)
【答案】C
【解析】将A(1,0),B(0,3)分别代入解析式得,![]() 解得,
解得, ![]() 则函数解析式为y=-x2-2x+3;
则函数解析式为y=-x2-2x+3;
将x=-1代入解析式可得其顶点坐标为(-1,4);当y=0时可得,-x2-2x+3=0;
解得,x1=-3,x2=1.
可见,抛物线与x轴的另一个交点是(-3,0);
由图可知,当x<-1时,y随x的增大而增大.
可见,C答案错误.故选C.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
相关题目
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?



