Question

【题目】△ABC中，AB=AC=5，BC=6，点D是BC上的一点，那么点D到AB与AC的距离的和为（　　）
A.5
B.6
C.4
D.

Answer 1

【答案】D
【解析】作△ABC的高CQ，AH，过C作CZ⊥DE交ED的延长线于Z，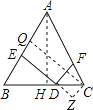

∵AB=AC=5，BC=6，AH⊥BC，
∴BH=CH=3，
根据勾股定理得：AH=4，
根据三角形的面积公式得：BCAH=ABCQ，
即：6×4=5CQ，
解得：CQ= ，
∵CQ⊥AB，DE⊥AB，CZ⊥DE，
∴∠CQE=∠QEZ=∠Z=90°，
∴四边形QEZC是矩形，
∴CQ=ZE，
∵∠QEZ=∠Z=90°，
∴∠QEZ+∠Z=180°，
∴CZ∥AB，
∴∠B=∠ZCB，
∵DF⊥AC，CZ⊥DE，
∴∠Z=∠DFC=90°，
∵AB=AC，
∴∠B=∠ACB，
∴∠ACB=∠ZCB，
∵CD=CD，∠ACB=∠ZCB，
∴△ZCD≌△FCD，
∴DF=DZ，
∴DE+DF=CQ=．
故选D．
【考点精析】本题主要考查了平行线的判定与性质和矩形的性质的相关知识点，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；矩形的四个角都是直角，矩形的对角线相等才能正确解答此题．