题目内容
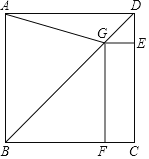
【题目】在△ABC 中,∠A=90°,AB=AC=![]() +1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
+1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
【答案】![]()
【解析】如图,过点P作MN∥BC,交AB于点M,交BC于点N,由PD⊥AB、PE⊥AC、∠A=90°,可得四边形AEPD为矩形,所以DP=AE;由∠A=90°,AB=AC=![]() +1,可得∠C=45°,再由MN∥BC,PE⊥AC可得△PEN为等腰直角三角形,所以PE=EN;又因PD+PE=PF,可得PF=AE+EN=AN;过点N作NG⊥BC与点G,可得PF=EG,△CGN为等腰直角三角形,设PF=EG=x,可得NG=
+1,可得∠C=45°,再由MN∥BC,PE⊥AC可得△PEN为等腰直角三角形,所以PE=EN;又因PD+PE=PF,可得PF=AE+EN=AN;过点N作NG⊥BC与点G,可得PF=EG,△CGN为等腰直角三角形,设PF=EG=x,可得NG=![]() x,因为AC=
x,因为AC=![]() +1,所以AN+NG=x+
+1,所以AN+NG=x+![]() x=
x=![]() +1,解得x=1;由此可得当PD+PE=PF时,点 P 运动所形成的图形是线段MN,根据勾股定理可求得MN的长度为
+1,解得x=1;由此可得当PD+PE=PF时,点 P 运动所形成的图形是线段MN,根据勾股定理可求得MN的长度为![]() .
.

练习册系列答案
相关题目
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?