题目内容
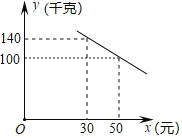
【题目】如图，在平面直角坐标系
中，直线
与
轴，
轴分别相交于点
，点
在射线
上，点
在射线
上，且
，以
为邻边作平行四边形
．设点的坐标为
，平行四边形在轴下方部分的面积为
．求：
（1）线段
的长；
（2）关于
的函数解析式，并直接写出自变量的取值范围．
【答案】（1）5；（2）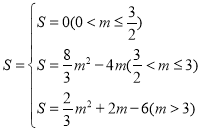
【解析】
（1）由直线y=-
与令x=0，或y=0，分别求出对应的y、x的值，从而确定A、B两点的坐标；
（2）分两种情况进行分别探究，①当
＜m≤3时，②当0＜m≤时，分别画出相应的图象，根据三角形相似，求出相应的边的长用含有m的代数式表示，再表示面积，从而确定在不同情况下S与m的函数解析式．
解：(1)当
时，
，
当
时，
，
∴直线
与
轴点交
，与
轴交点
∴
，
，
∴
，
因此：线段
的长为5．
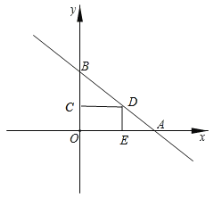
（2）当
时，如图，
∵
，
，
∴
，
由
∽
得：
，即：
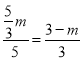，解得：
；
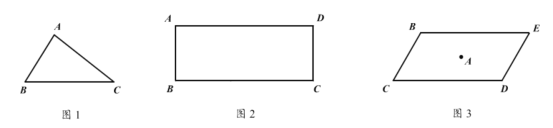
①当
时，如图1所示：
，此时点
在
的内部，
（）；
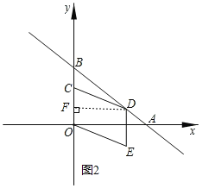
②当
时，如图2所示：过点
作
，垂足为
，
此时在轴下方的三角形与
全等，
∵
∽
，
∴
，
∴
，同理：
，
∴
，
∴
，
即：
，（）
③当
时，如图3所示：过点作
轴，
轴，垂足为
，
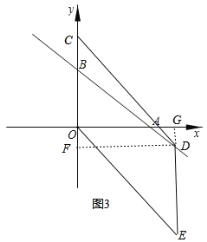
同理得：，，
∴
，
，
∴
∴
答：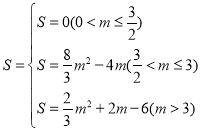
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛，试卷题目共10题，每题10分．现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100．
整理数据：
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据：
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题：
（1）请直接写出表格中
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；
（3）为了让学生重视安全知识的学习，学校将给竞赛成绩满分的同学颁发奖状，该校七年级新生共570人，试估计需要准备多少张奖状？
【题目】某校为了解八年级男生“立定跳远”成绩的情况，随机选取该年级部分男生进行测试，以下是根据测试成绩绘制的统计图表的一部分．
成绩等级 | 频数（人） | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息，解答下列问题
（1）被测试男生中，成绩等级为“优秀”的男生人数为 人，成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %；
（2）被测试男生的总人数为 人，成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %；
（3）若该校八年级共有180名男生，根据调查结果，估计该校八年级男生成绩等级为“良好”的学生人数．
