题目内容
【题目】如图,AB,CD是圆O的直径,AE是圆O的弦,且AE∥CD,过点C的圆O切线与EA的延长线交于点P,连接AC.
(1)求证:AC平分∠BAP;
(2)求证:PC2=PAPE;
(3)若AE-AP=PC=4,求圆O的半径.

【答案】(1)证明见解析;(2)证明见解析;(3)5.
【解析】
(1)OA=OC,则∠OCA=∠OAC,CD∥AP,则∠OCA=∠PAC,即可求解;
(2)证明△PAC∽△PCE,即可求解;
(3)利用△PAC∽△CAB、PC2=AC2-PA2,AC2=AB2-BC2,即可求解.
解:(1)∵OA=OC,∴∠OCA=∠OAC,
∵CD∥AP,
∴∠OCA=∠PAC,
∴∠OAC=∠PAC,
∴AC平分∠BAP;
(2)连接AD,
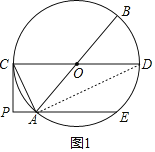
∵CD为圆的直径,
∴∠CAD=90°,
∴∠DCA+∠D=90°,
∵CD∥PA,
∴∠DCA=∠PAC,
又∠PAC+∠PCA=90°,
∴∠PAC=∠D=∠E,
∴△PAC∽△PCE,
∴![]() ,
,
∴PC2=PAPE;
(3)AE=AP+PC=AP+4,
由(2)得16=PA(PA+PA+4),
PA2+2PA-8=0,解得,PA=2,
连接BC,

∵CP是切线,则∠PCA=∠CBA,
Rt△PAC∽Rt△CAB,
![]() ,而PC2=AC2-PA2,AC2=AB2-BC2,
,而PC2=AC2-PA2,AC2=AB2-BC2,
其中PA=2,
解得:AB=10,
则圆O的半径为5.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】每年5月份是心理健康宣传月,某中学开展以“关心他人,关爱自己”为主题的心理健康系列活动.为了解师生的心理健康状况,对全体2000名师生进行了心理测评,随机抽取20名师生的测评分数进行了以下数据的整理与
①数据收集:抽取的20名师生测评分数如下
85,82,94,72,78,89,96,98,84,65,73,54,83,76,70,85,83,63,92,90.
②数据整理:将收集的数据进行分组并评价等第:
分数x |
|
|
|
|
|
人数 | 5 | a | 5 | 2 | 1 |
等第 |
|
|
|
|
|
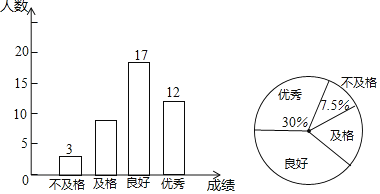
③数据绘制成不完整的扇形统计图:
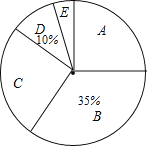
④依据统计信息回答问题
(1)统计表中的 .
(2)心理测评等第![]() 等的师生人数所占扇形的圆心角度数为 .
等的师生人数所占扇形的圆心角度数为 .
(3)学校决定对![]() 等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?
等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?