题目内容
【题目】两条抛物线![]() 与
与![]() 的顶点相同.
的顶点相同.
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物找
是抛物找![]() 在第四象限内图象上的一动点,过点
在第四象限内图象上的一动点,过点![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)设抛物线![]() 的顶点为点
的顶点为点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,问在
,问在![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使线段
,使线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,且点
,且点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)先求得![]() 顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
(2)作![]() 轴,设
轴,设![]() ,得到
,得到![]() 与a的函数关系式,即可解答;
与a的函数关系式,即可解答;
(3)过点![]() 作
作![]() 于点
于点![]() .接下来分情况讨论①当点
.接下来分情况讨论①当点![]() 在顶点
在顶点![]() 的下方时,可得
的下方时,可得![]() ;②当点
;②当点![]() 在顶点
在顶点![]() 的上方时,可得
的上方时,可得![]() ;
;
(1)![]() 的顶点为
的顶点为![]() ,
,
∵抛物线![]() 与
与![]() 的顶点相同
的顶点相同
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)作![]() 轴,
轴,
设![]() ,
,
∵![]() 在第四象限,
在第四象限,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() 的最大值为
的最大值为![]() ;
;
(3)假设![]() 的对称轴上存在点
的对称轴上存在点![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
①当点![]() 在顶点
在顶点![]() 的下方时,
的下方时,
∵![]() ,
,![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]() ,
,
设点![]() ,
,
∴![]() ,
,![]() ,
,
可知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ,
,
②当点![]() 在顶点
在顶点![]() 的上方时,同理可得
的上方时,同理可得![]() ;
;
综上所述:![]() 或
或![]() ;
;

【题目】 郑州外国语中学为了解学生课下阅读所用时间的情况,从各年级学生中随机抽查了一部分学生进行统计,下面是针对此次统计所制作的不完整的频数分布表和频数分布直方图,请根据图表信息回答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |
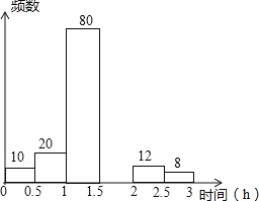
(1)表中a=______b=______;
(2)请补全频数分布直方图;
(3)样本中,学生日阅读所用时间的中位数落在第______组;
(4)该校共有学生3000人,请估计学生日阅读量不少于1.5小时的人数.
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.