题目内容
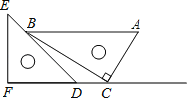
【题目】如图,△ABC内接于半圆,AB为直径,过点A作直线MN,若∠MAC=∠ABC.

(1)求证:MN是半圆的切线.
(2)设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F,求证:FD=FG.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据圆周角定理推论得到∠ACB=90°,即∠ABC+∠CAB=90°,而∠MAC=∠ABC,则∠MAC+∠BCA=90°,即∠MAB=90°,根据切线的判定即可得到结论;
(2)连AD,根据圆周角定理推论得到∠ABC=90°,由DE⊥AB得到∠DEB=90°,则∠1+∠5=90°,∠3+∠4=90°,又
D是弧AC的中点,即弧CD=弧DA,得到∠3=∠5,于是∠1=∠4,利用对顶角相等易得∠1=∠2,则有FD=FG.
(1)证明:∵AB为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
而∠MAC=∠ABC,
∴∠MAC+∠BCA=90°,即∠MAB=90°,
∴MN是半圆的切线;
(2)如图
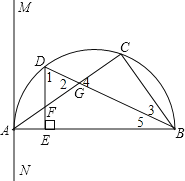
∵AB为直径,
∴∠ACB=90°,
而DE⊥AB,
∴∠DEB=90°,
∴∠1+∠5=90°,∠3+∠4=90°,
∵D是弧AC的中点,即弧CD=弧DA,
∴∠3=∠5,
∴∠1=∠4,
而∠2=∠4,
∴∠1=∠2,
∴FD=FG.

练习册系列答案
相关题目