题目内容
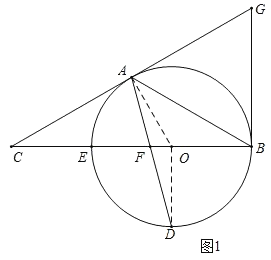
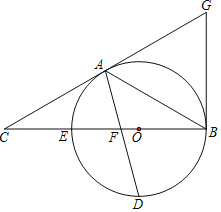
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC,
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
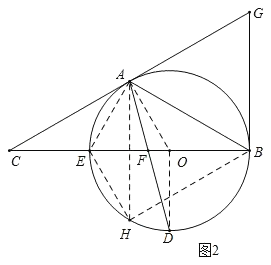
(3)过点B作⊙O的切线交CA的延长线于G,如果连接AE,将线段AC以直线AE为对称轴作对称线段AH,点H正好落在⊙O上,连接BH,求证:四边形AHBG为菱形.
【答案】(1)见解析;(2)6;(3)见解析
【解析】
(1)连接OA,OD,证∠OAF=∠D,∴∠CAF=∠CFA=∠OFD,∠EOD=90°,可推出∠CAF+∠∠OAF=90°,进一步推出结论;
(2)如图1,设半径为r,在Rt△OFD中,通过勾股定理即可求出半径的值;
(3)连接EH,证△CAE≌△HAE,推出△AEO是等边三角形,进一步证明△ABH和△ABG是等边三角形,即可推出结论.
解:(1)证明:如图1,连接OA,OD,
则∠OAF=∠D,
∵D为BE的下半圆弧的中点,
∴![]() ,
,
∴∠EOD=∠BOD=![]() ×180°=90°,
×180°=90°,
∴∠OFD+∠D=90°,
∵CA=CF,
∴∠CAF=∠CFA=∠OFD,
∴∠CAF+∠∠OAF=90°,
即∠CAO=90°,
∴OA⊥CA,
∴AC是⊙O的切线;
(2)如图1,设半径为r,
则OF=BF﹣OB=8﹣r,
∵在Rt△OFD中,OF2+OD2=DF2,
∴(8﹣r)2+r2=(![]() )2,
)2,
解得,r1=6,r2=2(舍去),
∴⊙O的半径为6;
(3)如图2,连接EH,
由对称性可知AC=AH,∠CAE=∠HAE,
又∵AE=AE,
∴△CAE≌△HAE(SAS),
∴∠C=∠EHA,
∵![]() ,
,
∴∠EHA=∠ABE,
∴∠C=∠ABE,
∵OA=OB,
∴∠OAB=∠OBA,
∵BE为⊙O的直径,
∴∠EAB=90°,
∴∠OAB+∠OAE=90°,
又∵∠CAE∠+∠OAE=90°,
∴∠CAE=∠OAB,
∴∠C=∠OBA=∠∠OAB=∠CAE,
∴AC=AB,
∴△CAE≌△BAO(ASA),
∴AE=AO=OE,
∴△AEO是等边三角形,
∴∠AEO=60°,
∴∠ABE=90°﹣∠AEO=30°,∠AHB=∠AEO=60°,
∴∠ABG=90°﹣∠ABE=60°,
∵CA=AH,CA=AB,
∴AH=AB,
又AHB=60°,
∴△ABH是等边三角形,
∴AB=BH=AH,
∵GB,GA是⊙O的切线,
∴GB=GA,
又∠ABG=60°,
∴△ABG是等边三角形,
∴AB=BG=AG,
∴BH=AH=BG=AG,
∴四边形AHBG是菱形.