题目内容
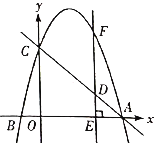
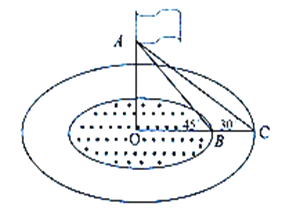
【题目】如图,小明在水平面E处,测得某建筑物AB的顶端A的仰角为42°,向正前方向走37米到达点D处,再往斜坡CD上走30米到达点C处,测得建筑物AB的顶端A的仰角为63.5°,已知斜坡CD的坡度为i=1:0.75,建筑物AB垂直于平台BC,平台BC与水平面DE平行,点A、B、C、D、E均在同一平面内,则建筑物AB的高度约为( )(精确到0.1米,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.0)
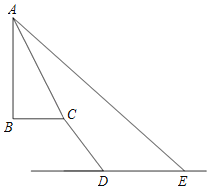
A.42.4米B.46.4米C.48.5米D.50.8米
【答案】B
【解析】
作CG⊥DE交ED的延长线于G,延长AB交ED的延长线于H,根据坡度的概念分别求出CG、DG,根据正切的定义用AB表示出BC,根据正切的定义列式计算,得到答案.
解:作CG⊥DE交ED的延长线于G,延长AB交ED的延长线于H,
则四边形BHGC为矩形,
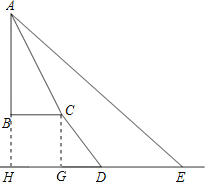
∴BH=CG,BC=HG,
设CG=x米,
∵斜坡CD的坡度为i=1:0.75,
∴DG=3x,
由勾股定理得,CD2=CG2+DG2,即302=(4x)2+(3x)2,
解得,x=6,
∴CG=24,DG=18,
在Rt△ABC中,tan∠ACB=![]() ,
,
∴BC=![]() ,
,
在Rt△AHE中,tan∠AEH=![]()
∴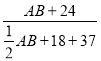 ≈0.9,
≈0.9,
解得,AB≈46.4,
故选:B.

练习册系列答案
相关题目