Question

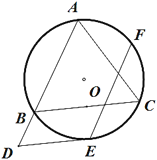
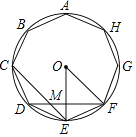
【题目】如图，⊙O的半径为2，正八边形ABCDEFGH内接于⊙O，对角线CE、DF相交于点M，则△MEF的面积是_____．

Answer 1

【答案】2﹣

【解析】

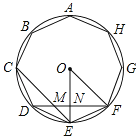
设OE交DF于N，由正八边形的性质得出DE＝FE，∠EOF＝＝45°，，由垂径定理得出∠OEF＝∠OFE＝∠OED，OE⊥DF，得出△ONF是等腰直角三角形，因此ON＝FN＝OF＝，∠OFM＝45°，得出EN＝OE﹣OM＝2﹣，证出△EMN是等腰直角三角形，得出MN＝EN，得出MF＝OE＝2，由三角形面积公式即可得出结果．

解：设OE交DF于N，如图所示：

∵正八边形ABCDEFGH内接于⊙O，

∴DE＝FE，∠EOF＝＝45°，，

∴∠OEF＝∠OFE＝∠OED，OE⊥DF，

∴△ONF是等腰直角三角形，

∴ON＝FN＝OF＝，∠OFM＝45°，

∴EN＝OE﹣OM＝2﹣，∠OEF＝∠OFE＝∠OED＝67.5°，

∴∠CED＝∠DFE＝67.5°﹣45°＝22.5°，

∴∠MEN＝45°，

∴△EMN是等腰直角三角形，

∴MN＝EN，

∴MF＝MN+FN＝ON+EN＝OE＝2，

∴△MEF的面积＝MF×EN＝×2×（2﹣）＝2﹣；

故答案为：2﹣．