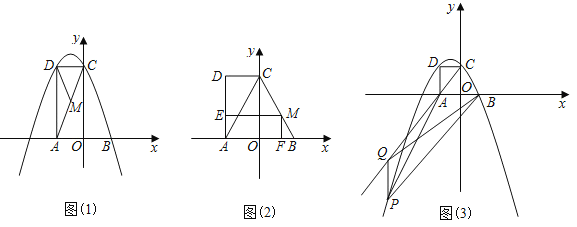题目内容
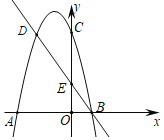
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C,D是二次函数图象上的一对对称点,一次函数的图象过点B,D,交y轴为E.
(1)求二次函数的解析式;
(2)求![]() 的值.
的值.
【答案】(1)y=﹣x2﹣2x+3;(2)![]() .
.
【解析】
(1)根据题意,设出抛物线的交点式,再根据抛物线过点C,可以求得该抛物线的解析式;
(2)根据(1)中的抛物线的解析式可以求得点D的坐标,从而可以求得直线BD的解析式,进而求得点E的坐标,再根据三角形相似,即可求得![]() 的值.
的值.
(1)设该函数的解析式为y=a(x+3)(x﹣1)
则3=a(0+3)(0﹣1),
解得,a=﹣1,
∴y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3,
即二次函数的解析式;是y=﹣x2﹣2x+3;
(2)∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴该函数的对称轴是直线x=﹣1,
∵点C(0,3),点C,D是二次函数图象上的一对对称点,
∴点D的坐标为(﹣2,3),
设过点B(1,0)、点D(﹣2,3)的直线的函数解析式为y=kx+b,
![]() ,得
,得![]() ,
,
即直线BD的解析式为y=﹣x+1,
当x=0时,y=﹣0+1=0,
即点E的坐标为(0,1),
作DF⊥AB于点F,
∵DF⊥AB,EO⊥AB于点O,
∴△BEO∽△BDF,
∴![]() =
=![]() ,
,
∵点B(1,0),点F(﹣2,0),
∴BO=1,BF=3,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.

练习册系列答案
相关题目