��Ŀ����
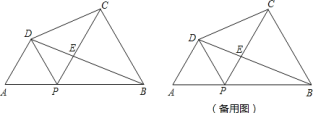
����Ŀ��һ��С������һ��������״��ȫ��ͬ�����ǵ���״��ͼ��ʾ�����жԽ���AC��BD����֪���ǵĶ�Ӧ��֮��Ϊ1��3��С���������Խ��ߵij��քeΪ12cm��14cm��
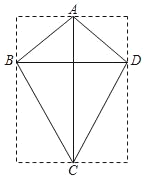
��1��С���ݵ�����Ƕ��٣�
��2������ڴ������װ��һ�����ӶԽǶ����ʮ�ֽ����ε�֧�żܣ���ô�������ö�IJ��ϣ���������ģ�
��3�������Ҫ�ò�ɫֽ���ǣ�����ɫֽ�Ǵ�һ�Ÿպø����������ݵľ��β�ɫֽ����ͼ��������ʾ���ü������ģ���ô���ĸ��Dzü������������õIJ�ɫֽ������Ƕ��٣�
���𰸡�(1)84��cm��2;(2) 78cm;(3) 756��cm��2
��������
��1�����������ε������ʽ��ʽ���㼴�ɣ�
��2���������������ε����ʵõ�A��C��=3AC=42cm��ͬ��B��D��=3BD=36cm�����ǵõ����ۣ�
��3�����ݾ��κ������ε������ʽ���ɵõ����ۣ�
�⣺��1����AC��BD��
��С���ݵ����S��![]() ACBD��
ACBD��![]() ��12��14��84��cm��2��
��12��14��84��cm��2��
��2����С������������״��ȫ��ͬ��
��������ݵ��ĸ�����ΪA����B����C����D����
���ABCD�ס�A��B��C��D����
�����ǵĶ�Ӧ��֮��Ϊ1��3��
��A��C����3AC��42cm��
ͬ��B��D����3BD��36cm��
����������42+36��78cm�IJ��ϣ�
��3�����ĸ��Dzü������������õIJ�ɫֽ����������ε����������ݵ������42��36��9��84��756��cm��2��

 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�