题目内容
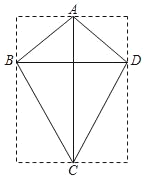
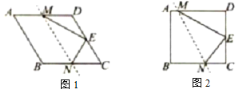
【题目】已知菱形纸片ABCD中,![]() ,点E是CD边的中点将该纸片折叠,使点B与点E重合,折痕交AD,BC边于点M,N,连接ME,NE.请从下面A,B两题中任选一题作答,我选择A.如图1,若
,点E是CD边的中点将该纸片折叠,使点B与点E重合,折痕交AD,BC边于点M,N,连接ME,NE.请从下面A,B两题中任选一题作答,我选择A.如图1,若![]() ,则ME的长为______;B.如图2,若
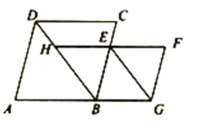
,则ME的长为______;B.如图2,若![]() ,则ME的长为_____.
,则ME的长为_____.
【答案】A.![]() B.
B.![]()
【解析】
(1)连接BD,BE,则△BCD是等边三角形,则BE⊥CD,由BE⊥MN,得到MN∥CD,则∠BNM=∠NCE=∠ENM=60°,得到△CNE是等边三角形,则CN=CE=2,得到N为BC中点,M为AD中点,连接AO,则ME=![]() ,由OD=2,CD=4,利用勾股定理求出CO,即可得到答案;
,由OD=2,CD=4,利用勾股定理求出CO,即可得到答案;
(2)连接BM,由折叠性质,得到BM=EM,在Rt△ABM中,![]() ,在Rt△EDM中,
,在Rt△EDM中,![]() ,设
,设![]() ,则
,则![]() ,根据等量关系,即可求出
,根据等量关系,即可求出![]() ,然后求出ME的长度.
,然后求出ME的长度.
解(1)如图,连接BD,BE,AC,
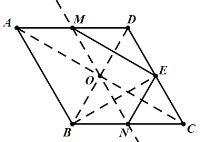
在菱形ABCD中,∠NCE=∠BAD=60°,BC=CD,
∴△BCD是等边三角形,
∵点E是CD中点,
∴BE⊥CD,
由折叠的性质,得到BE⊥MN,
∴MN∥CD,
∴∠BNM=∠NCE=∠ENM=60°,
∴∠ENC=∠NCE=∠NEC=60°,
∴△CNE是等边三角形,
∴CN=CE=2,
∴点N是BC的中点,
∴点M是AD的中点,
∴ME=![]() ,
,
∵在Rt△ODC中,![]() ,CD=4,
,CD=4,
由勾股定理,得![]() ,
,
∴ME=![]() ;
;
故答案为:![]() .
.
(2)如图,连接BM,
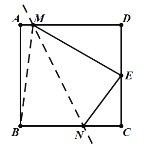
由折叠的性质,得BM=EM,
∵∠A=90°,则四边形ABCD是正方形,
∴∠D=∠A=90°,AB=AD=4,
在Rt△ABM和Rt△EDM中,由勾股定理,得:
![]() ,
, ![]()
设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴AM=![]() ,
,
∴![]() ,
,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=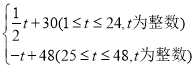 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.