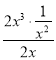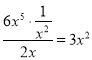题目内容
【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )
A.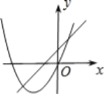 B.
B.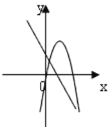 C.
C.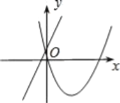 D.
D.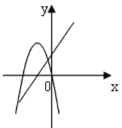
【答案】C
【解析】
首先根据图形中给出的一次函数图象确定a、b的符号,进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意,根据选项逐一讨论解析,即可解决问题.
解答
A. 对于直线y=ax+b来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2bx来说,对称轴x=![]() >0,应在y轴的右侧,故不合题意,图形错误;
>0,应在y轴的右侧,故不合题意,图形错误;
B. 对于直线y=ax+b来说,由图象可以判断,a<0,b>0;而对于抛物线y=ax2bx来说,对称轴x=![]() <0,应在y轴的左侧,故不合题意,图形错误;
<0,应在y轴的左侧,故不合题意,图形错误;
C. 对于直线y=ax+b来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2bx来说,图象开口向上,对称轴x=![]() >0,应在y轴的右侧,故符合题意;
>0,应在y轴的右侧,故符合题意;
D. 对于直线y=ax+b来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2bx来说,图象开口向下,a<0,故不合题意,图形错误;
故选:C.

练习册系列答案
相关题目
【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=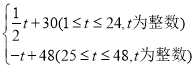 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.