Question

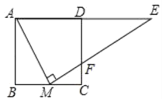
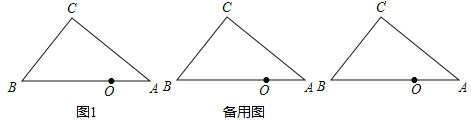
【题目】如图：在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，O是AB上一点，且AO＝2．

（1）求点O到直线AC的距离OH的长；

（2）若P是边AC上一个动点，作PQ⊥OP交线段BC于Q（不与B、C重合），设AP＝x，CQ＝y，试求y关于x的函数解析式，并写出定义域；

（3）在（2）的条件下，当AP为多少时能使△OPQ与△CPQ相似．

Answer 1

【答案】（1）OH＝；（2）y＝﹣x2+x﹣（＜x＜4）；（3）当△OPQ与△CPQ相似时，AP为．

【解析】

（1）通过证明△AOH∽△ABC，即可判断出，求出OH的长度；

（2）通过证明△AOD∽△ABC，可得：，从而求出AD、PD的长度各是多少，然后根据相似三角形判定的方法，判断出△POD∽QPC，即可推得，据此求出y关于x的函数解析式．并写出函数定义域即可．

（3）根据题意，分两种情况：当OQ∥AC时；当PQ平分∠CQO时；然后根据相似三角形的性质，分类讨论，求出AP长是多少即可．

解：（1）如图1，过点O作OH⊥AC，

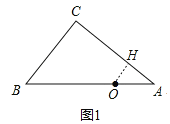
∵∠C＝90°，AC＝4，BC＝3，

∴AB＝＝＝5，

∵∠A＝∠A，∠ACB＝∠AHO＝90°，

∴△AOH∽△ABC，

∴，

即，

∴OH＝；

（2）如图2，过点O作OD⊥AC，

由（1）可得OD＝，

∵∠BCA＝∠ODA＝90°，∠A＝∠A，

∴△AOD∽△ABC，

∴，

∴，

∴AD＝，

∴PD＝x﹣，

∵PQ⊥OP，

∴∠OPD+∠CPQ＝90°，

又∵∠PQC+∠CPQ＝90°，

∴∠OPD＝∠PQC，且∠ACB＝∠PDO＝90°，

∴△POD∽△QPC，

∴，

∴

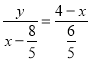
∴y＝﹣x2+x﹣

由题意可知：AD＜AP＜AC

∴＜x＜4

（3）如图3，当OQ∥AC时，△OPQ∽△QCP，

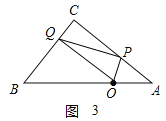
∵OQ∥AC，

∴，

∴＝，

∴CQ＝，

∴＝﹣x2+x﹣，

∴x＝，

∴AP＝；

如图4，作PE⊥OQ于点E，

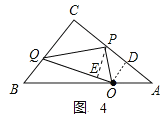
当PQ平分∠CQO时，△OPQ∽△PCQ，

∵∠CQP＝∠PQE，PC⊥BC，PE⊥OQ，

∴PC＝PE，

∵∠POQ＝∠CPQ，∠DOP＝∠CPQ，

∴∠POQ＝∠DOP，

又∵PD⊥OD，PE⊥OE，

∴PD＝PE，

∴PC＝PD，

即点P为CD的中点，

由AP﹣AD＝AC﹣AP，

∴2AP＝AC+AD＝4+，

∴AP＝，

综上所述：当△OPQ与△CPQ相似时，AP为．