题目内容
【题目】在平面直角坐标系中,将点A(3,4)绕原点旋转90°得点B,则点B坐标为 .
【答案】(﹣4,3)或(4,﹣3).
【解析】
试题分析:有两种情况:当逆时针旋转时,B点在B1位置上,过B1N⊥x轴于N,过A作AM⊥x轴于M,当顺时针旋转时,B到B2位置上,过B2Q⊥y轴于Q,求出AM=4,OM=3,
将点A(3,4)绕原点旋转90°得点B,根据全等三角形的判定得出△B1NO≌△OMA,△AOM≌△B2OQ,根据全等三角形的性质得出B1N=OM=3,ON=AM=4,OQ=OM=3,B2Q=AM=4,即可得出答案.
解: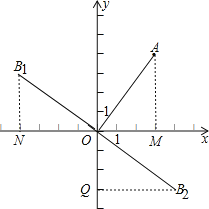
有两种情况:当逆时针旋转时,B点在B1位置上,过B1N⊥x轴于N,过A作AM⊥x轴于M,当顺时针旋转时,B到B2位置上,过B2Q⊥y轴于Q,
则∠B1NO=∠AM0=∠B2QO=90°,
∵A(3,4),
∴AM=4,OM=3,
∵将点A(3,4)绕原点旋转90°得点B,
∴∠B1OA=∠AOB2=90°,OA=OB1=OB2,
∴∠B1+∠B1ON=90°,∠B1ON+∠AOM=90°,∠A+∠AOM=90°,∠AOM+∠B2OM=90°,∠B2OM+∠B2OQ=90°,
∴∠B1=∠AOM,∠AOM=∠B2OQ,
在△B1NO和△OMA中
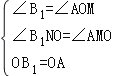
∴△B1NO≌△OMA(AAS),
∴B1N=OM=3,ON=AM=4,
∴此时B的坐标为(﹣4,3);
同理△AOM≌△B2OQ,
则OQ=OM=3,B2Q=AM=4,
此时B的坐标为(4,﹣3).
故答案为:(﹣4,3)或(4,﹣3).

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目