题目内容
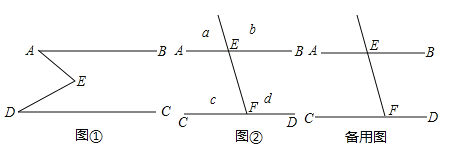
【题目】如图①，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．
（1）探究猜想：
①若∠A=20°，∠D=40°，则∠AED= °
②猜想图①中∠AED，∠EAB，∠EDC的关系，并用两种不同的方法证明你的结论．
（2）拓展应用：
如图②，射线FE与l1，l2交于分别交于点E、F，AB∥CD，a，b，c，d分别是被射线FE隔开的4个区域（不含边界，其中区域a，b位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（任写出两种，可直接写答案）．
【答案】（1）① 60；②∠AED=∠A+∠D；（2）当P在a区域时，∠PEB=∠PFC+∠EPF；当P点在b区域时，∠PFC=∠PEB+∠EPF；当P点在区域c时，∠EPF+∠PEB+∠PFC=360°；当P点在区域d时，∠EPF=∠PEB+∠PFC．
【解析】试题分析：（1）①根据平行线的性质求出角的度数即可；②本题的方法一，利用平行线的性质和外角的性质即可得出结论；方法二利用平行线的性质得出即可；（2）本题分四种情况讨论，画出图形，利用平行线的性质和三角形外角性质得出结论即可.
试题解析：
（1）① ∠AED=60°
②∠AED=∠A+∠D，
证明：方法一、延长DE交AB于F，如图1，
∵AB∥CD，
∴∠DFA=∠D，
∴∠AED=∠A+∠DFA；
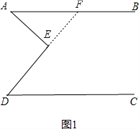
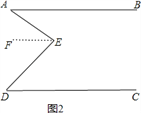
方法二、过E作EF∥AB，如图2，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠A=∠AEF，∠D=∠DEF，
∴∠AED=∠AEF+∠DEF=∠A+∠D；
（2）任意写一个。
当P在a区域时，如图3，∠PEB=∠PFC+∠EPF；
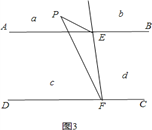
当P点在b区域时，如图4，∠PFC=∠PEB+∠EPF；
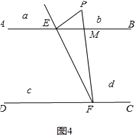
当P点在区域c时，如图5，∠EPF+∠PEB+∠PFC=360°；
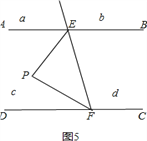
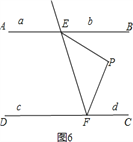
当P点在区域d时，如图6，∠EPF=∠PEB+∠PFC．
