题目内容
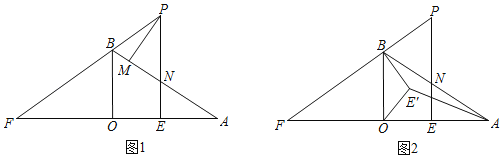
【题目】如图1,∠AOB=90°,OA=4,OB=3,点E在线段OA上,EP⊥OA交AB于点N,PM⊥AB,直线PB与AO交于点F.
(1)若AN=3,S△PBN=8,求PN的长;
(2)设△PMN的周长为C1,△AEN的周长为C2,若△PFE~△BAO且![]() =
=![]() ,求OE的长;
,求OE的长;
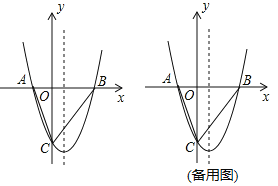
(3)如图2,若OE=2,将线段OE绕点O逆时针旋转得到OE',旋转角为α (0°<α<90°),连接E'A、E'B,求E'A+![]() E'B的最小值.
E'B的最小值.
【答案】(1)PN=10;(2)OE=![]() ;(3)
;(3)![]()
【解析】
(1)证明△PMN∽△AOB,可得![]() ,由此即可解决问题.
,由此即可解决问题.
(2)如图1﹣2中,作BK⊥PN于K,设PN=6k.利用等腰三角形的性质证明PK=KN=3k,BK=4k,BN=5k,由△PMN∽△AEN,且![]() ,推出
,推出![]() ,推出AN=10k,可得AB=15k=5,解得k=
,推出AN=10k,可得AB=15k=5,解得k=![]() ,由此即可解决问题.
,由此即可解决问题.
(3)如图3中,在BO上取一点的K,使得OK=![]() ,连接KE′,KA.证明△OKE′∽△OE′B,推出E′K:BE′=OE′:OB=2:3,推出E′K=
,连接KE′,KA.证明△OKE′∽△OE′B,推出E′K:BE′=OE′:OB=2:3,推出E′K=![]() BE′,推出AE′+
BE′,推出AE′+![]() BE′=AE′+KE′,由AE′+KE′≥AK,求出AK即可解决问题.
BE′=AE′+KE′,由AE′+KE′≥AK,求出AK即可解决问题.
解:(1)如图1﹣1中,
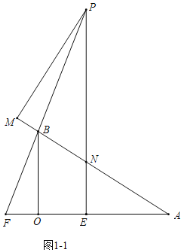
在Rt△AOB中,∵OB=3,OA=4,
∴AB=![]() ,
,
∵AN=3,
∴BN=AB﹣AN=2,
∵PM⊥AM,
∴S△PBN=![]() =8,
=8,
∴PM=8,
∵PE⊥OA,
∴∠AEN=∠AOB=∠M=90°,
∴OB∥PN,
∴∠ABO=∠PNM,
∴△PMN∽△AOB,
∴![]() ,
,
∴![]() ,
,
∴PN=10.
(2)如图1﹣2中,作BK⊥PN于K,设PN=6k.
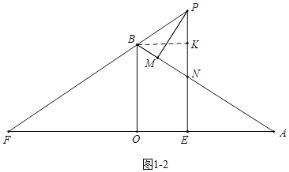
∵△PFE∽△BAO,
∴∠F=∠A,
∵PK∥AF,
∴∠PBK=∠∠KBN=∠A,
∴∠PBK=∠KBN,
∵BK⊥PN,
∴∠BKP=∠BKN=90°,
∴∠BPK+∠PBK=90°,∠BNK+∠KBN=90°,
∴∠BPK=∠BNK,
∴BP=BN,
∴PK=KN=3k,BK=4k,BN=5k,
∵△PMN∽△AEN,且![]() ,
,
∴![]() ,
,
∴AN=10k,
∴AB=15k=5,
∴k=![]() ,
,
∴BK=![]() ,
,
∵四边形BOEK是矩形,
∴OE=BK=![]() .
.
(3)如图3中,在BO上取一点的K,使得OK=![]() ,连接KE′,KA.
,连接KE′,KA.
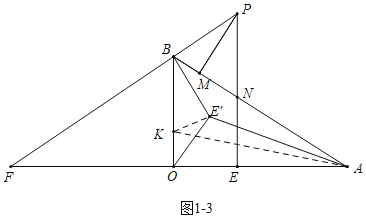
∵OE′2=4,OKOB=![]() ×3=4,
×3=4,
∴OE′2=OKOB,
∴![]() ,
,
∵∠KOE′=∠BOE′,
∴△OKE′∽△OE′B,
∴E′K:BE′=OE′:OB=2:3,
∴E′K=![]() BE′,
BE′,
∴AE′+![]() BE′=AE′+KE′,
BE′=AE′+KE′,
∵AE′+KE′≥AK,AK=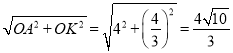 ,
,
∴AE′+![]() BE′≥
BE′≥![]() ,
,
∴E'A+![]() E'B的最小值为
E'B的最小值为![]() .
.