题目内容
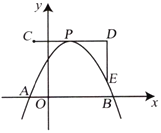
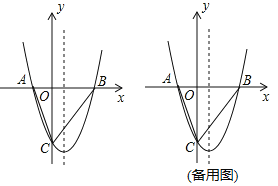
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于C点,OA=2,OC=6,连接AC和BC.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标;
(3)点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;
【答案】(1)y=x2﹣x﹣6;(2)点D的坐标为(![]() ,﹣5);(3)△BCE的面积有最大值
,﹣5);(3)△BCE的面积有最大值![]() ,点E坐标为(
,点E坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)先求出点A,C的坐标,再将其代入y=x2+bx+c即可;
(2)先确定BC交对称轴于点D,由两点之间线段最短可知,此时AD+CD有最小值,而AC的长度是定值,故此时△ACD的周长取最小值,求出直线BC的解析式,再求出其与对称轴的交点即可;
(3)如图2,连接OE,设点E(a,a2﹣a﹣6),由式子S△BCE=S△OCE+S△OBE﹣S△OBC即可求出△BCE的面积S与a的函数关系式,由二次函数的图象及性质可求出△BCE的面积最大值,并可写出此时点E坐标.
解:(1)∵OA=2,OC=6,
∴A(﹣2,0),C(0,﹣6),
将A(﹣2,0),C(0,﹣6)代入y=x2+bx+c,
得![]() ,
,
解得,b=﹣1,c=﹣6,
∴抛物线的解析式为:y=x2﹣x﹣6;
(2)在y=x2﹣x﹣6中,
对称轴为直线x=![]() ,
,
∵点A与点B关于对称轴x=![]() 对称,
对称,
∴如图1,可设BC交对称轴于点D,由两点之间线段最短可知,此时AD+CD有最小值,
而AC的长度是定值,故此时△ACD的周长取最小值,
在y=x2﹣x﹣6中,
当y=0时,x1=﹣2,x2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx﹣6,
将点B(3,0)代入,
得,k=2,
∴直线BC的解析式为y=2x﹣6,
当x=![]() 时,y=﹣5,
时,y=﹣5,
∴点D的坐标为(![]() ,﹣5);
,﹣5);
(3)如图2,连接OE,
设点E(a,a2﹣a﹣6),
S△BCE=S△OCE+S△OBE﹣S△OBC
=![]() ×6a+
×6a+![]() ×3(﹣a2+a+6)﹣
×3(﹣a2+a+6)﹣![]() ×3×6
×3×6
=﹣![]() a2+
a2+![]() a
a
=﹣![]() (a﹣
(a﹣![]() )2+
)2+![]() ,
,
根据二次函数的图象及性质可知,当a=![]() 时,△BCE的面积有最大值
时,△BCE的面积有最大值![]() ,
,
当a=![]() 时,
时,![]()
∴此时点E坐标为(![]() ,﹣
,﹣![]() ).
).



 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案