题目内容
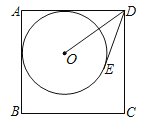
【题目】如图，⊙O与正方形ABCD的两边AB，AD相切，且DE与⊙O相切于点E．若AB＝7，DO＝5，则DE的长度为_____．
【答案】4或3
【解析】
设⊙O与AB、AD分别切于M、N两点，连接OM、ON，则可证得四边形AMON为正方形，利用切线长定理可求得DN=DE，设AN=x，则可得x2+(7﹣x)2=52，则可求得AN，则可求得DE．
设⊙O与AB、AD分别切于M、N两点，连接OM、ON，
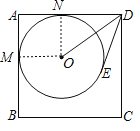
∵四边形ABCD为正方形，
∴∠A=90°，AD=AB=7，
∵AD、AB与⊙O相切，
∴∠ANO=∠AMO=∠A=90°，且AM=AN，
∴四边形AMON为正方形，
设AN=x，
∵ON2+DN2=OD2，
∴
，
解得
=3或4，
∴AN=3或4，
∵DE与⊙O相切，
∴DN=DE=4或3，
故答案为：4或3．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
