题目内容
【题目】已知抛物线的顶点为![]() ,且过点
,且过点![]() .直线
.直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
(1)求该抛物线的解析式;
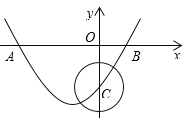
(2)以线段![]() 为直径的圆与射线
为直径的圆与射线![]() 相交于点
相交于点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先设出抛物线的顶点式,再将点A的坐标代入可得出结果;
(2)先求出射线![]() 的解析式为
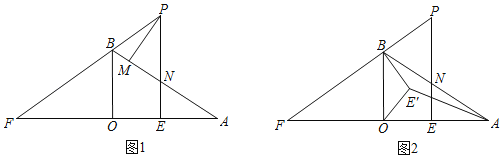
的解析式为![]() ,可设点P的坐标为(x,x).圆与射线OA相交于两点,分两种情况:①如图1当
,可设点P的坐标为(x,x).圆与射线OA相交于两点,分两种情况:①如图1当![]() 时,构造
时,构造![]() 和
和![]() ,再在直角三角形中利用勾股定理,列方程求解;②如图2,当
,再在直角三角形中利用勾股定理,列方程求解;②如图2,当![]() 时,构造
时,构造![]() 和
和![]() ,再在直角三角形中利用勾股定理,列方程求解.
,再在直角三角形中利用勾股定理,列方程求解.
解:(1)根据顶点设抛物线的解析式为:![]() ,
,
代入点![]() ,得:
,得:![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
设直线![]() 的解析式为:
的解析式为:![]() ,
,
分别代入![]() 和
和![]() ,
,
得:![]() ,
,
直线![]() 的解析式为:
的解析式为:![]() ;
;
(2)由(1)得:直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,得
,得![]() ,
,![]()
由题意可得射线![]() 的解析式为
的解析式为![]() ,
,
![]() 点
点![]() 在射线
在射线![]() 上,则可设点
上,则可设点![]() ,
,
由图可知满足条件的点![]() 有两个:
有两个:
①当![]() 时,构造
时,构造![]() 和
和![]() ,
,
可得:如图1:
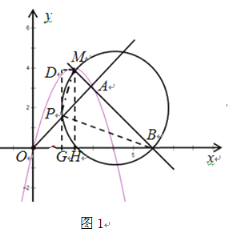
由图可得,![]() ,
,![]() ,
,
![]() .
.
在Rt△PMD中,![]() ,
,
在Rt△PBG中,![]() ,
,
在Rt△BMH中,![]() ,
,
![]() 点
点![]() 在以线段
在以线段![]() 为直径的圆上,
为直径的圆上,![]() ,
,
可得:![]() ,
,
即:![]() .
.
整理,得:
![]() ,解得:
,解得:![]() ;
;
![]() ,
,![]() .
.
![]() ;
;
②当![]() 时,如图2,构造
时,如图2,构造![]() 和
和![]() ,可得:
,可得:
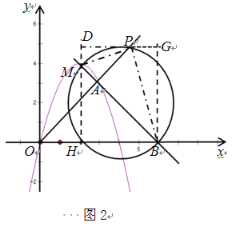
同理,根据BM2=BP2+PM2,可得方程:
42+42=(6-x)2+x2+(x-2)2+(x-4)2,化简得,
![]() ,解得:
,解得:![]() ,
,
∵![]() .
.
![]() .
.
综上所述,符合题目条件的![]() 点有两个,其坐标分别为:
点有两个,其坐标分别为:![]() 或
或![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目