题目内容
【题目】如图,在边长为5的正方形ABCD中,点E在BC边上,连接AE,过D作DF//AE交BC的延长线于点F,过点C作CG⊥DF于点G,延长AE、GC交于点H,点P是线段DG上的任意一点(不与点D、点G重合),连接CP,将△CPG沿CP翻折得到![]() ,连接
,连接![]() . 若CH=1,则
. 若CH=1,则![]() 长度的最小值为__________.
长度的最小值为__________.

【答案】![]()
【解析】
如图,作DM⊥AE于M,首先证明四边形DMHG是正方形,求出正方形DMHG的边长,以及AC的长,因为点P在线段DG上运动时,点G′在以C为圆心,CG为半径的圆上运动,所以当A、G′、C共线时,AG′最小.由此即可解决问题.
解:如图,作DM⊥AE于M.设CG=x,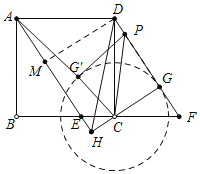
∵AH∥DF,GH⊥DF,
∴∠MHG=∠HGD=∠DMH=90°,
∴四边形DMHG是矩形,
∵∠ADC=∠MDG=90°,
∴∠ADM=∠CDG,
在△ADM和△CDG中,
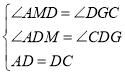 ,
,
∴△ADM≌△CDG(AAS),
∴DM=DG,
∴四边形DMHG是正方形,
∴GH=DG,
∵CH=1,CG=x,
∴DG=CG+HC=x+1,
在Rt△DCG中,![]() ,
,
∴x=3,x=-4(舍去),
∴CG′=CG=3,
在Rt△ADC中,AC= ![]() ,
,
∵点P在线段DG上运动时,点G′在以C为圆心,CG为半径的圆上运动,
∴当A、G′、C共线时,AG′最小,
∴AG′的最小值为AC-CG′= ![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目